Sudoku 1
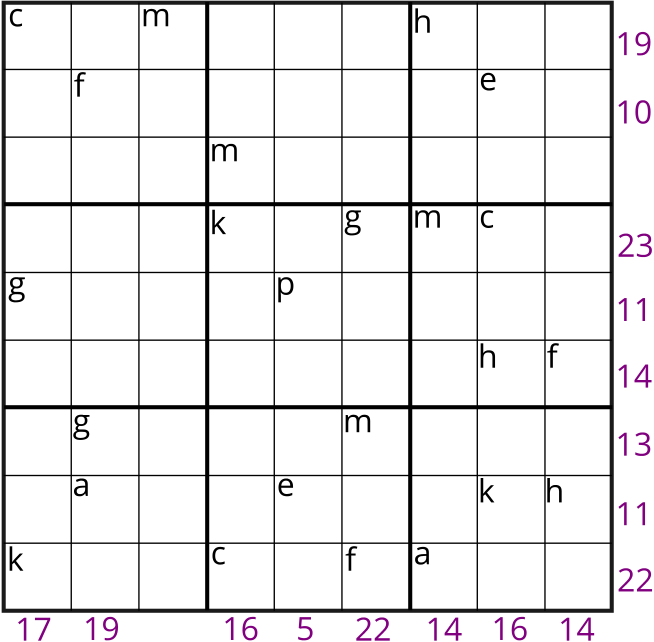
Here is one way we could solve this puzzle.
Here are the 16 equations:
\(c+m+h=19\)
\(f+e=10\)
\(k+g+m+c=23\)
\(g+p=11\)
\(h+f=14\)
\(g+m=13\)
\(a+e+k+h=11\)
\(k+c+f+a=22\)
\(c+g+k=17\)
\(f+g+a=19\)
\(m+k+c=16\)
\(p+e=5\)
\(g+m+f=22\)
\(h+m+a=14\)
\(e+c+h+k=16\)
\(f+h=14\)
We first look at the most simple equations with only two unknowns.
Equation 12 says that \(p+e=5\). This means that both \(p\) and \(e\) must be less than or equal to \(4\).
Equation 2 says that \(f+e=10\), and since we know that \(e\) is less than or equal to \(4\), this means that \(f\ge6\).
Equation 4 says that \(g+p=11\), so we must have \(g\ge7\).
Equation 5/16 tells us that \(h+f=14\), so \(h\le 8\).
Now look at equation 7, \(a+e+k+h=11\). The only four different positive whole numbers that can add up to \(11\) are \(1+2+3+5\). So we must have that each of \(a\), \(e\), \(k\), \(h\) must be one of \(1\), \(2\), \(3\), \(5\). We know that \(e\le4\), but we now know that \(e\le3\), and so \(2\le p\le4\). Also, since \(h\le 8\) and must add up with a number less than or equal to \(9\) to make \(14\) by equation 5, we have that \[h=5.\] So by equation 5, \[f=9.\] But now by equation 2 \[e=1,\] and by equation 12 \[p=4,\] which we can put into equation 4 to find that \[g=7.\] We now use equation 6 to deduce that \[m=6.\]
It remains to deduce the values of the letters \(a\) and \(k\) (each of which we know must take one of the values \(2\) and \(3\)) and \(c\). The only number left for \(c\) is therefore \(8\)—we can check using equation 1 \[c+m+h=c+6+5=19 \implies c=8 \;\checkmark\]
We use equation 14 to check what value \(a\) takes: \[h+m+a=5+6+a=14 \implies a=3.\]
So we must have \(k=2\), but we can double check: by equation 11, \[m+k+c=6+k+8=16 \implies k=2 \checkmark\]
| Letter | Number |
|---|---|
| \(a\) | \(3\) |
| \(c\) | \(8\) |
| \(e\) | \(1\) |
| \(f\) | \(9\) |
| \(g\) | \(7\) |
| \(h\) | \(5\) |
| \(k\) | \(2\) |
| \(m\) | \(6\) |
| \(p\) | \(4\) |
So the Sudoku now looks like

The solution to the Sudoku is

Sudoku 2
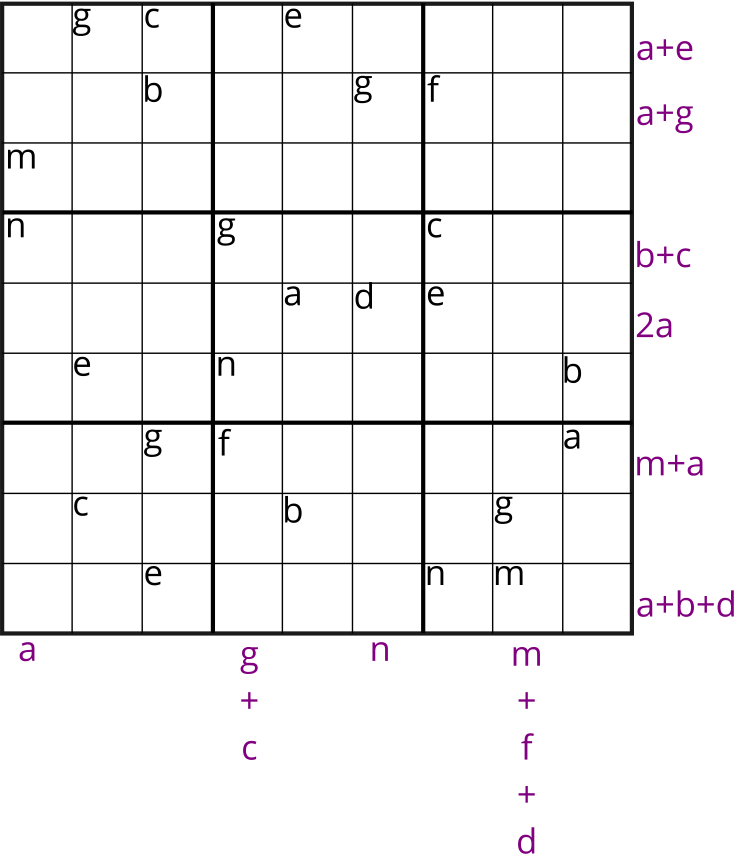
For the second Sudoku, we have the following 10 equations:
\(m+n=a\)
\(g+n+f=g+c\implies n+f=c\)
\(g+d=n\)
\(g+m=m+f+d \implies g=f+d\)
\(g+c+e=a+e\implies g+c=a\)
\(b+g+f=a+g\implies b+f=a\)
\(n+g+c=b+c\implies n+g=b\)
\(a+d+e=2a\implies d+e=a\)
\(g+f+a=m+a\implies g+f=m\)
\(e+n+m=a+b+d\)
Equations 3 and 4 share two of the same unknowns, so this seems like a good place to start. Eliminating \(g\) yields the equation \[f+d=n-d \implies n=2d+f.\]
From equation 2, \(n=c-f\), so we further see that \[c-f=2d+f \implies c=2d+2f.\] From this equation we see that \(c\) is even, and \(c\ge 6\) (since the smallest values \(d\) and \(f\) can take are \(1\) and \(2\)), so we have that either \(c=6\) and the \(d\) and \(f\) are equal to \(1\) and two or \(c=8\) and then \(d\) and \(f\) are equal to \(1\) and \(3\).
Now look at equation 5, \(g+c=a\). The largest value that \(g\) can take is \(3\), if \(c=6\). The only other option therefore, is that \(g=2\), since we have already established that one of \(d\) and \(f\) must be \(1\). But since we must have that \(a\le9\), this means that we must have \[c=6,\] and therefore each of \(d\) and \(f\) must take one of the values \(1\) and \(2\). This excludes the possibility of \(g\) taking the value \(2\), so we must have \[g=3,\] which tells us that \[a=9\] by equation 5.
Equation 1 says that \(m+n=a=9\). Since the values \(1\) to \(3\) are already taken, the only way we can make \(9\) with two numbers is with \(4\) and \(5\). So each of \(m\) and \(n\) must take one of the values \(4\) and \(5\). The other letters and numbers we have left are \(b\) and \(e\) and \(7\) and \(8\). We will look at equation 10, \(e+n+m=a+b+d\) to determine which values they should take. We know that \(n+m=a=9\), so we can simplify this equation to consider \(e=b+d\), which says that \(b < e\), so since we knew each of \(b\) and \(e\) were one of \(7\) and \(8\), we now know that \[b=7 \text{ and } e=8,\] which further tells us that we must have \[d=1,\] and so we must also have \[f=2.\] Equation 3 now says that \(3+1=n\), so we finally know that \[n=4 \text{ and } m=5.\]
| Letter | Number |
|---|---|
| \(a\) | \(9\) |
| \(b\) | \(7\) |
| \(c\) | \(6\) |
| \(d\) | \(1\) |
| \(e\) | \(8\) |
| \(f\) | \(2\) |
| \(g\) | \(3\) |
| \(m\) | \(5\) |
| \(n\) | \(4\) |
So the Sudoku to solve is

The solution to the Sudoku is


