We have provided a set of functions cards for you to cut out and sort. For each of these functions, try to decide whether or not the function is odd or even.
Using the symmetry of the graphs we can see which functions are even or odd. We can also consider \(f(-x)\) and \(f(x)\) to verify this. Do you notice anything about the following?
- powers of \(x\)
- transformations of graphs
- asymptotes
| Even functions | Odd functions |
|---|---|
| \(f(x)=x^2+1\) | \(f(x)=x\) |
| \(f(x)=-1\) | \(f(x)=\sqrt[3]{x}\) |
| \(f(x)=\vert x \vert-3\) | \(f(x)=0\) |
| \(f(x) = 1-x^2+x^4\) | \(f(x)= x^3-x\) |
| \(f(x)=0\) | \(f(x)=x+\dfrac{1}{x}\) |
| \(f(x)= \dfrac{1}{x^2-1}\) | |
| \(f(x)=\dfrac{1}{x^2+1}\) |
Do the graphs of any of the odd functions have a line of symmetry as well as rotational symmetry? Do the graphs of any of the even functions have rotational symmetry?
You may have noticed that only one of the functions we provided is both even and odd. Do you think there are other functions that are both even and odd?
If the function is neither odd nor even, is its graph symmetric in some other way?
There are five functions that are neither odd nor even. The graphs of some of these functions have lines of symmetry or rotational symmetry about points other than \((0,0).\)
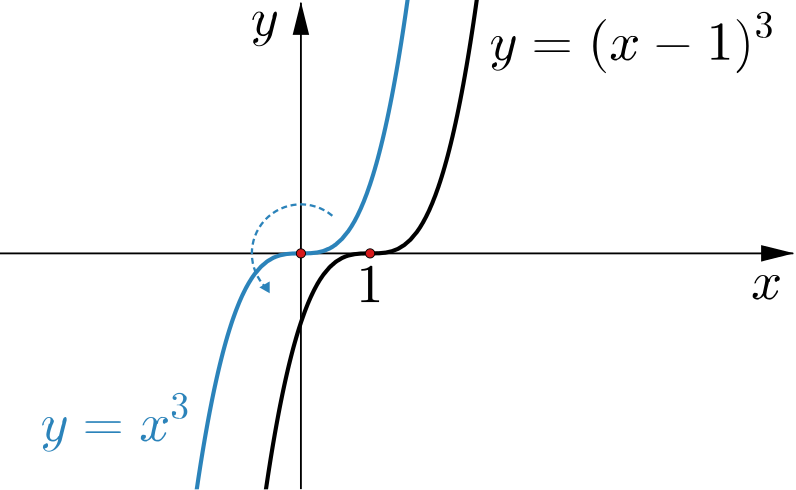
- The graph of the function \(f(x)=(x-1)^3\) is a translation of the graph \(y=x^3\) parallel to the \(x\)-axis. We know that \((-x)^3=-x^3\), so \(f(x)\) is a translation of an odd function and its graph has rotational symmetry about the point \((1,0).\)
We can apply a similar argument about transformations of functions or think directly about the symmetry of \(f(x)=2x^2+4x\) and \(y=2x+1.\)
- The function \(f(x)=\dfrac{3}{1+x}\) is quite interesting. You might see its graph as a translation of \(y=\dfrac{3}{x}\) and we often describe this as a stretch of a \(y=\dfrac{1}{x}\) graph parallel to the \(y\)-axis.
What different rotational and line symmetries does the graph \(y=\dfrac{1}{x}\) have?
What happens to these symmetries when we transform the graph?
You might find it interesting to explore graphs of the form \(xy=c\) using Desmos.
Another point of view
We have focused on using transformations to help make sense of the symmetry of graphs of functions which aren’t odd or even. There are plenty of other ways to think about these functions and properties that they have in common. You might like to look at Function squares or Two-way functions to explore these ideas.

