In this interactivity, you can move the points \(A\), \(B\), \(C\) and \(D\) around the circumference of the circle, with \(D\) between \(B\) and \(C\).
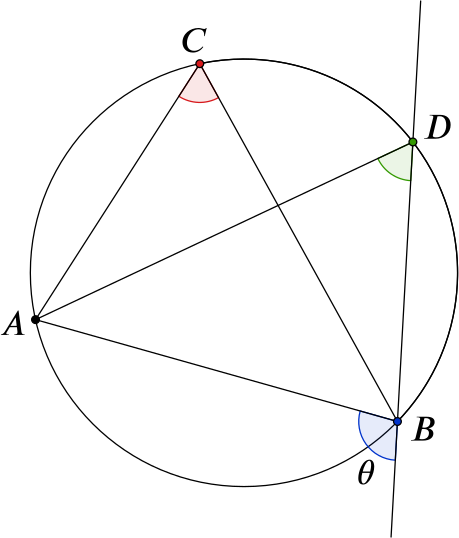
Three angles are marked.
What can you say about the angles at \(C\) and \(D\)?
What happens to these angles if you move \(C\) or \(D\), keeping \(A\) and \(B\) fixed?
How do you know this?
In this situation, we have a fixed chord \(AB\) and the angles at the circumference \(\angle ACB\) and \(\angle ADB\) on the same side of the chord. This reminds us of the theorem that angles at the circumference on the same side of the same chord are equal. Therefore \(\angle ACB\) is constant regardless of where \(C\) lies, and likewise \(\angle ADB\) is constant. Furthermore, because of this theorem, they are also equal: \(\angle ACB=\angle ADB\).
- What happens to the exterior angle at \(B\) (shown in blue) as \(D\) approaches \(B\)?
We have labelled the angle at \(B\) as \(\theta\). This makes it easier to talk about it. It is equal to the sum of the opposite two interior angles of the triangle \(ABD\), that is \(\theta=\angle BAD+\angle ADB\).
Why is this the case? It is because of two standard angle theorems:
\(\angle BAD+\angle ADB+\angle ABD=180^\circ\), since the angles in a triangle sum to \(180^\circ\).
\(\theta+\angle ABD=180^\circ\), because angles on a straight line sum to \(180^\circ\).
Then equating these expressions and subtracting \(\angle ABD\) shows that \(\theta=\angle BAD+\angle ADB\).
As the point \(D\) moves towards \(B\), the angle \(\angle BAD\) tends towards zero, and so \(\theta\) tends to \(\angle ADB\), which is the same as \(\angle ACB\).
Alternatively, we might say that as \(D\) moves towards \(B\), the chord \(AD\) tends to the chord \(AB\), so the angles \(\angle ADB\) and \(\theta\) become closer and closer to each other. Since \(\angle ADB=\angle ACB\) remains fixed, the exterior angle \(\theta\) tends towards \(\angle ACB\).
- Which other circle theorem can you deduce from this?
Exploring the interactivity seems to suggest that the line \(BD\) becomes closer and closer to the tangent to the circle at \(B\). This is, indeed, the case; we explore tangents in more detail at Calculus of Powers.
We can say that in the limit, as \(D\) approaches \(B\), the line \(BD\) tends to the tangent to the circle at \(B\).
Also, as we have just observed, in the limit, the exterior angle \(\theta\) tends to \(\angle ACB\). On the other hand, the line \(BD\) tends to the tangent at \(B\), so the angle \(\theta\) tends to the angle between the tangent at \(B\) and the chord \(BA\).
So in the limit, we see that the (exterior) angle between \(BA\) and the tangent at \(B\) equals \(\angle ACB\).
This is known as the alternate segment theorem.

