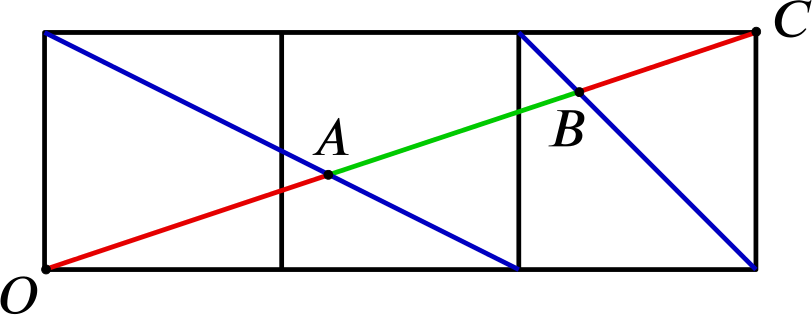
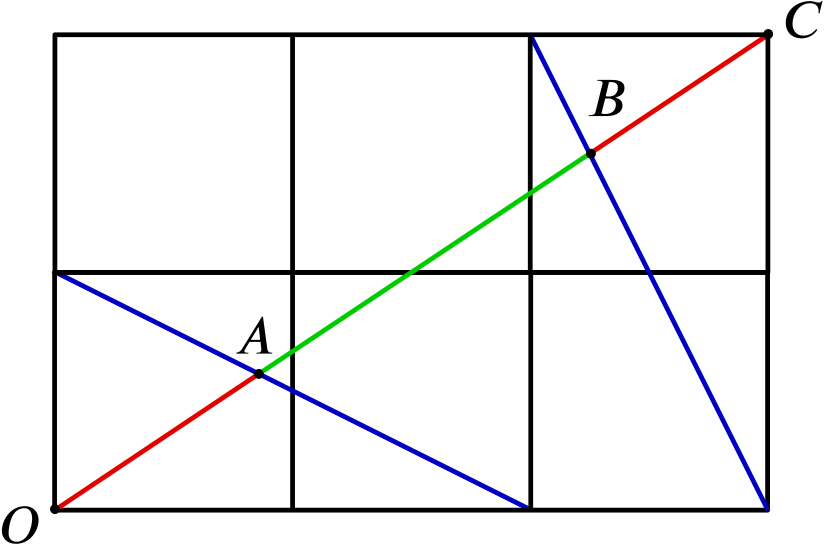
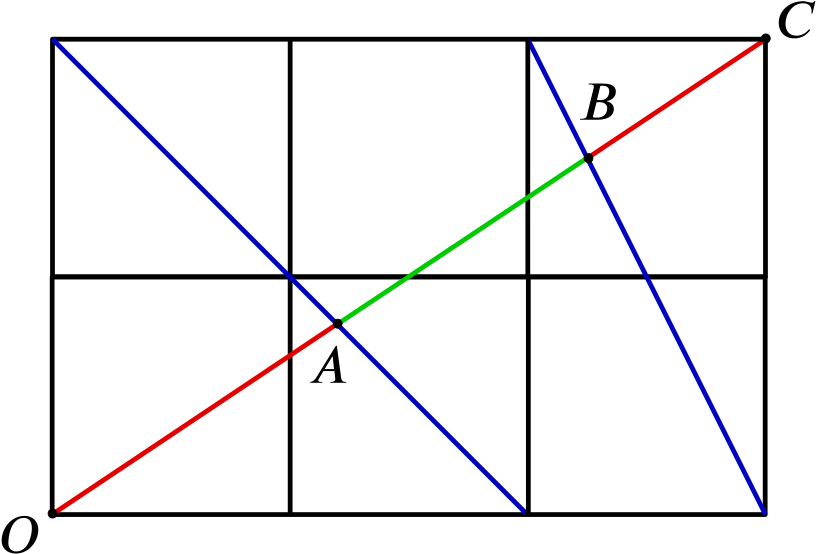
Can you work out the ratio \(\frac{AB}{OC}\) in each of these cases?
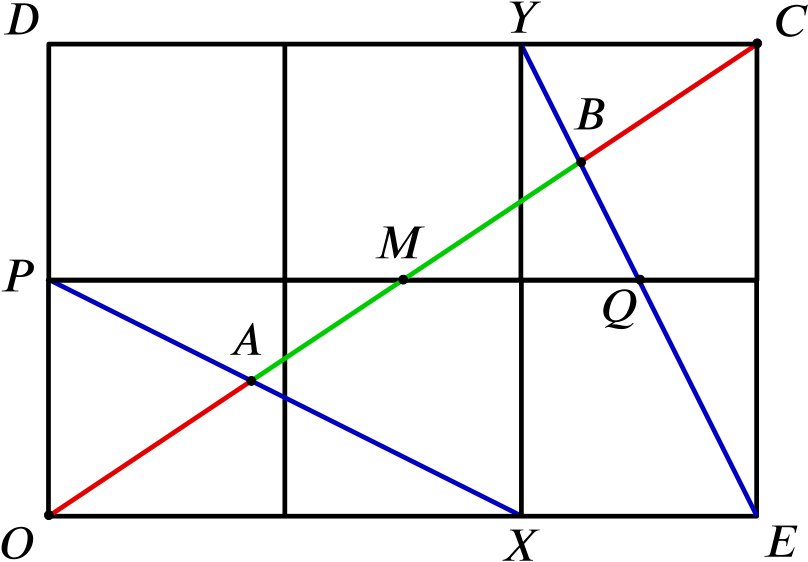
It’s helpful to label some more key points, so that we can talk about them conveniently. Let \(X\) be the lower end point and \(Y\) the upper end point of the vertical line segment between \(A\) and \(B\), as shown.
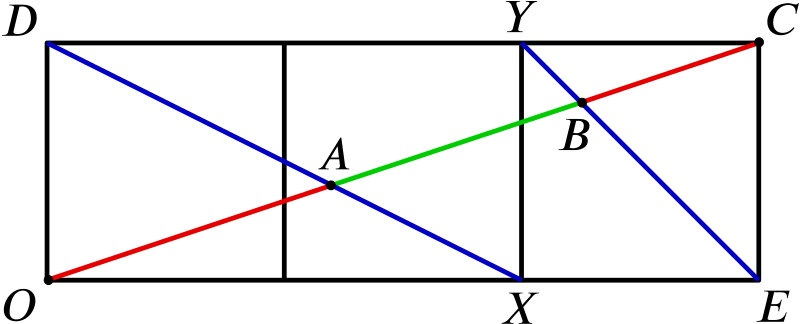
It looks as though triangles \(OAX\) and \(CAD\) might be similar, so let’s try to prove that.
Opposite angles at a point are the same, so angles \(OAX\) and \(CAD\) are the same. Also, \(DC\) and \(OE\) are parallel, so angles \(AOX\) and \(ACD\) are the same. So triangles \(OAX\) and \(CAD\) have the same angles, so they are similar.
You might be familiar with this as the ‘AAA’ reason for two triangles to be similar: all three angles are the same.
Now we can use that to deduce that certain ratios are the same. More precisely, \[\frac{OA}{CA} = \frac{OX}{CD}.\]
Here’s a tip when dealing with similar triangles. When we said that triangles \(OAX\) and \(CAD\) are similar, the points were in the right order. That is, vertex \(O\) in triangle \(OAX\) corresponds to vertex \(C\) in triangle \(CAD\), vertex \(A\) in triangle \(OAX\) corresponds to vertex \(A\) in triangle \(CAD\), and vertex \(X\) in triangle \(OAX\) corresponds to vertex \(D\) in triangle \(CAD\). Being careful about that ordering when we wrote down the similar triangles makes it easier to be clear about which sides of the triangles correspond.
But we know that \(OX = \frac{2}{3} CD\), so \[\frac{OA}{CA} = \frac{2}{3}.\]
This is useful, because we can now find \(OA\) in terms of \(OC\). Clearly \(OA + AC = OC\), so we must have \(OA = \frac{2}{5} OC\) (and also \(AC = \frac{3}{5} OC\), although we don’t need that).
This seems helpful, especially if we can also find the length of \(OB\). But that will be OK, by doing something very similar to the argument above.
Similarly, triangle \(CBY\) is similar to triangle \(OBE\), so \[\frac{CB}{OB} = \frac{CY}{OE} = \frac{1}{3},\] and so \(CB = \frac{1}{3} OB\), so \(OB = \frac{3}{4} OC\).
Now \[\frac{AB}{OC} = \frac{OB - OA}{OC} = \frac{3}{4} - \frac{2}{5} = \frac{7}{20}.\]
At this point, we should behave like mathematicians by trying to answer this question as efficiently as possible. How can we use our work on the first part to help? We can start to see which points to label and where we might look for helpful similar triangles.
We see that triangles \(AMP\) and \(AOX\) have the same angles and so are similar, so \[\frac{OA}{MA} = \frac{OX}{MP}.\] We know that \(OX = \frac{2}{3} OE\) and \(MP = \frac{1}{2} OE\), so \[\frac{OA}{MA} = \frac{\frac{2}{3}}{\frac{1}{2}} = \frac{4}{3},\] so \[OA = \frac{4}{3} MA.\] But \(OA + AM = \frac{1}{2} OC\), so \(OA = \frac{4}{7} OM = \frac{2}{7} OC\).
We would also like to find \(OB\), perhaps by finding \(BC\).
Triangles \(BCY\) and \(BMQ\) are similar. In fact, we see that \(MQ = \frac{1}{3} DC = YC\), because \(M\) and \(Q\) are each at the midpoints of their respective sides of squares, so triangles \(BCY\) and \(BMQ\) are congruent.
So \(BC = BM = \frac{1}{2} CM = \frac{1}{4} OC\).
Now \[\frac{AB}{OC} = \frac{OC - OA - BC}{OC} = 1 - \frac{2}{7} - \frac{1}{4} = \frac{28 - 8 - 7}{28} = \frac{13}{28}.\]
Pictures 1 and 2 are genuinely different, so we had to tweak our solution a bit. But Picture 3 looks a lot like Picture 1, just stretched to be a bit taller, so maybe we don’t need to do much more work…
Picture 3 is the same as Picture 1, but stretched to double the height. In our solution above for Picture 1, we considered only ratios throughout, so in fact exactly the same argument works for Picture 3, and so \[\frac{AB}{OC} = \frac{7}{20}\] in this case too.