Here are some triangles.
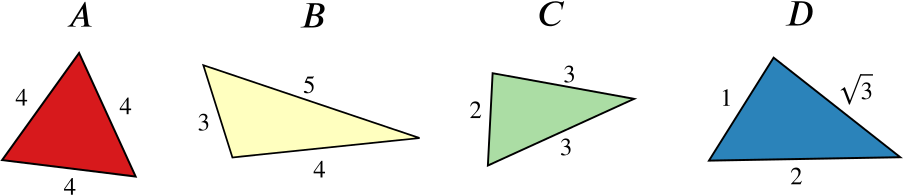
The diagrams are not to scale.
Can you find …
- … a triangle similar to triangle A with perimeter \(6\)?
Triangle A has perimeter \(4 + 4 + 4 = 12\), so we want to scale by factor \(6/12 = 1/2\), so we should choose the triangle with side lengths \(2\), \(2\) and \(2\).
- … a triangle similar to triangle B with perimeter \(6\)?
Triangle B has perimeter \(3 + 4 + 5 = 12\) (like triangle A), so we again use factor \(1/2\), so we should choose the triangle with side lengths \(3/2\), \(2\) and \(5/2\).
- … a triangle similar to triangle C with perimeter \(6\)?
Triangle C has perimeter \(3 + 3 + 2 = 8\), so we want to scale by factor \(6/8 = 3/4\). So we should choose the triangle with side lengths \(9/4\), \(9/4\) and \(3/2\).
- … a triangle similar to triangle D with perimeter \(6\)?
Triangle D has perimeter \(1 + 2 + \sqrt{3} = 3 + \sqrt{3}\), so we want to scale by factor \[\frac{6}{3 + \sqrt{3}} = \frac{6(3 - \sqrt{3})}{(3 + \sqrt{3})(3 - \sqrt{3})} = 3 - \sqrt{3}.\] So we should choose the triangle with side lengths \(3 - \sqrt{3}\), \(6 - 2\sqrt{3}\) and \(-3 + 3\sqrt{3}\).
- … a triangle similar to triangle A with area \(10\)?
We need to remember that when we scale the lengths of a triangle by a certain factor, we scale the area of the triangle by the square of that factor. So we must allow for that.
Triangle A has area \(4\sqrt{3}\), so we want to scale by factor \[\sqrt{\frac{10}{4\sqrt{3}}} = \sqrt{\frac{5\sqrt{3}}{6}}.\] So we should choose the triangle with side lengths \(4\sqrt{\frac{5\sqrt{3}}{6}}\), \(4\sqrt{\frac{5\sqrt{3}}{6}}\) and \(4\sqrt{\frac{5\sqrt{3}}{6}}\).
- … a triangle similar to triangle B with area \(10\)?
Triangle B has area \(6\), so we want to scale by factor \[\sqrt{\frac{10}{6}} = \frac{\sqrt{15}}{3}.\] So we should choose the triangle with side lengths \(\sqrt{15}\), \(\frac{4\sqrt{15}}{3}\) and \(\frac{5\sqrt{15}}{3}\).
- … a triangle similar to triangle C with area \(10\)?
Triangle C has area \(2\sqrt{2}\), so we want to scale by factor \[\sqrt{\frac{10}{2\sqrt{2}}} = \sqrt{\frac{5\sqrt{2}}{2}}.\] So we should choose the triangle with side lengths \(\sqrt{10\sqrt{2}}\), \(3\sqrt{\frac{5\sqrt{2}}{2}}\), \(3\sqrt{\frac{5\sqrt{2}}{2}}\).
- … a triangle similar to triangle D with area \(10\)?
Triangle D has area \(\frac{\sqrt{3}}{2}\), so we want to scale by factor \[\sqrt{\frac{10}{\sqrt{3}/2}} = \sqrt{\frac{20}{\sqrt{3}}} = \frac{2\sqrt{5}}{\sqrt[4]{3}}.\] So we should choose the triangle with side lengths \(\frac{2\sqrt{5}}{\sqrt[4]{3}}\), \(\frac{4\sqrt{5}}{\sqrt[4]{3}}\) and \(\frac{2\sqrt{15}}{\sqrt[4]{3}}\).
- … a right-angled triangle similar to one of triangles A, B, C, D with area \(12\)?
Of the four given triangles, only triangles B and D are right-angled. We can check that using Pythagoras’s theorem, since the side lengths \(3\), \(4\) and \(5\) satisfy his equation, as do the side lengths \(1\), \(\sqrt{3}\) and \(2\).
Let’s find a triangle similar to B with area \(12\). And we can do that using the same approach as earlier.
Triangle B has area \(6\), so we want to scale by factor \[\sqrt{\frac{12}{6}} = \sqrt{2}.\] So we should choose the triangle with side lengths \(3\sqrt{2}\), \(4\sqrt{2}\) and \(5\sqrt{2}\).
- … an isosceles triangle similar to one of triangles A, B, C, D with area \(12\)?
Of the four given triangles, only triangles A and C are isosceles. We could choose either, but let’s choose C and save A for later since it’s equilateral too.
Triangle C has area \(2\sqrt{2}\), so we want to scale by factor \[\sqrt{\frac{12}{2\sqrt{2}}} = \sqrt{3\sqrt{2}}.\] So we should choose the triangle with side lengths \(2\sqrt{3\sqrt{2}}\), \(3\sqrt{3\sqrt{2}}\) and \(3\sqrt{3\sqrt{2}}\).
- … an equilateral triangle similar to one of triangles A, B, C, D with area \(12\)?
Our only option here is triangle A.
Triangle A has area \(4\sqrt{3}\), so we want to scale by factor \[\sqrt{\frac{12}{4\sqrt{3}}} = \sqrt[4]{3}.\] So we should choose the triangle with side lengths \(4\sqrt[4]{3}\), \(4\sqrt[4]{3}\) and \(4\sqrt[4]{3}\).
- … a scalene triangle similar to one of triangles A, B, C, D with area \(12\)?
Here we can choose between triangles B and D. Since we’ve already done B, let’s pick D.
Triangle D has area \(\frac{\sqrt{3}}{2}\), so we want to scale by factor \[\sqrt{\frac{12}{\sqrt{3}/2}} = \sqrt{8\sqrt{3}} = 2\sqrt{2\sqrt{3}}.\] So we should choose the triangle with side lengths \(2\sqrt{2\sqrt{3}}\), \(4\sqrt{2\sqrt{3}}\) and \(2\sqrt{6\sqrt{3}}\).
- … a right-angled triangle with area \(12\) that is not similar to any of triangles A, B, C, D?
We have lots of choice here, we just have to make sure that our right-angled triangle isn’t similar to triangle B or D(it definitely won’t be similar to either of the others).
Let’s try to be lazy when constructing an example. An easy way to make a triangle have area \(12\) is to give it base \(12\) and height \(2\), for example, and then we can use Pythagoras to finish off.
Choose the triangle with side lengths \(2\), \(12\) and \(\sqrt{2^2 + 12^2} = \sqrt{4 + 144} = \sqrt{148} = 2\sqrt{37}\). The side lengths satisfy Pythagoras’s equation so the triangle is right-angled, and its area is \(12\). It is easy to check that it is not similar to triangle B or triangle D, by looking at ratios of two sides (e.g. \(\frac{3}{4} \neq \frac{2}{12}\)).
- … an isosceles triangle with area \(12\) that is not similar to any of triangles A, B, C, D?
We need to avoid both A and C here. It should be quite straightforward to build an isosceles triangle with area \(12\), by picking the base and height and then finding the missing side length.
Choose the isosceles triangle with base \(2\) (as one side of the triangle) and height \(12\). The other sides have length \(\sqrt{1^2 + 12^2} = \sqrt{145}\). This is clearly isosceles, clearly has area \(12\), and cannot be similar to triangle C (since they have the same base but different heights).
- … an equilateral triangle with area \(12\) that is not similar to any of triangles A, B, C, D?
This is a bit tricky…
Every equilateral triangle is similar to every other equilateral triangle! So any equilateral triangle will be similar to A, so there is no triangle that meets the criteria.
- … a scalene triangle with area \(12\) that is not similar to any of triangles A, B, C, D?
There are lots and lots of examples here. Again, a nice approach might be to specify the base and height, since they determine the area, and then just to make sure that the triangle is not isosceles or right-angled. The hardest part might be calculating the side lengths!

