A perfect fit
Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Printable/supporting materials Printable version Fullscreen mode Teacher notes

Solution

How can you accurately construct the inscribed circle of a right-angled triangle?

Diagram shows blue circle inside a right-angled triangle, touching in 3 places

We might start by thinking about the sequence of labelled diagrams shown below (these are suggested in the suggestion section and a printable version is available here).

Diagram	Description
	Mark the centre of the inscribed circle. Draw lines to show the radii at the points where the circle touches the outer triangle.
	The outer triangle is tangent to the inscribed circle in three places. A tangent meets a radius at a right-angle. Draw lines from the centre of the circle to the vertices of the outer triangle, dividing the outer triangle into six, smaller, right-angled triangles.
	The pink triangle is congruent to the green triangle by RHS (they both contain a right-angle, share a common hypotenuse, and a side length of \(r\)). The pink triangle is also congruent to the green triangle by SSS as they share a side length of \(r\), a common hypotenuse, and a third side length (tangents to a circle from the same point are equal in length). The pink and green triangles together form a kite. The shared hypotenuse bisects angle \(A\) of the outer triangle.
	The pink triangle is congruent to the green triangle by RHS. The pink and green triangle are both isosceles (they each have two sides of length \(r\)) and together they form a square. The shared hypotenuse bisects angle \(C\) of the outer triangle.
	The pink triangle is congruent to the green triangle by RHS. The pink and green triangles together form a kite. The shared hypotenuse bisects angle \(B\) of the outer triangle.

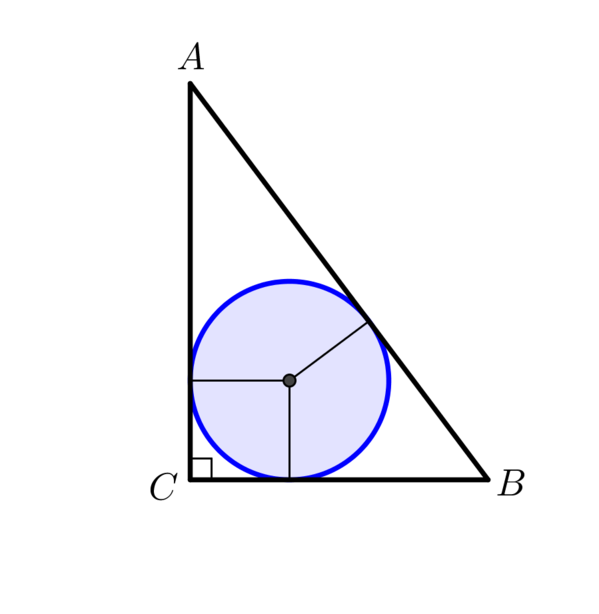
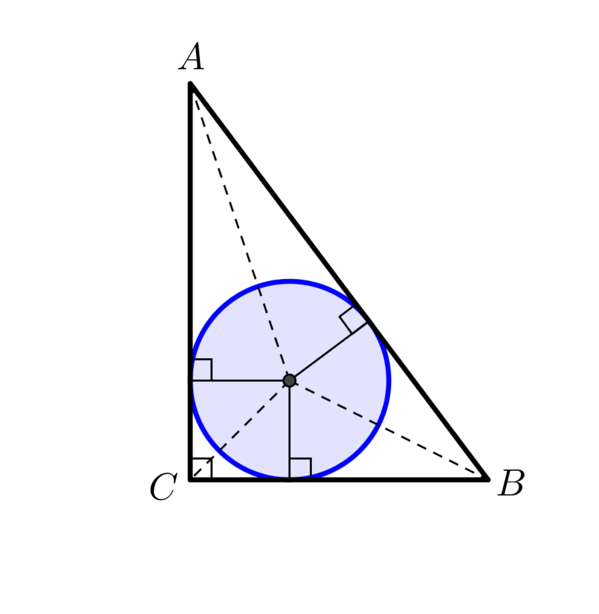
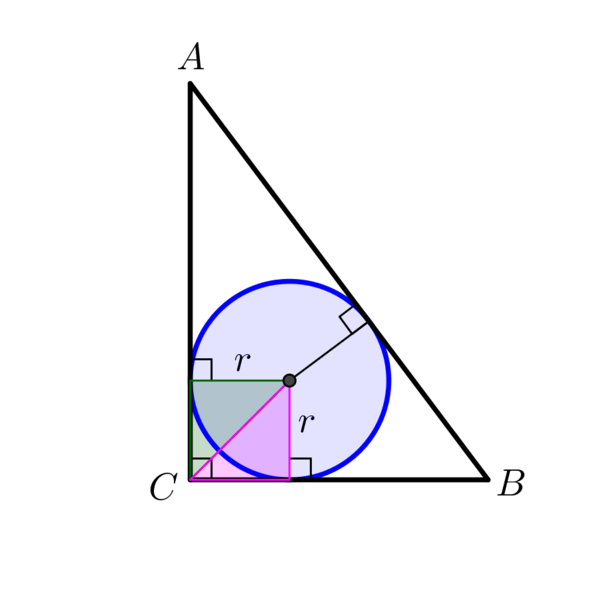
At this point we can summarise that the centre of the inscribed circle lies at the intersection of the angle bisectors of the outer triangle.

In order to accurately construct the inscribed circle we must therefore first construct any two of the angle bisectors of \(A\), \(B\), and \(C\). If we then construct a perpendicular line from the centre to one edge of the outer triangle, we can use this to set the radius on our pair of compasses and hence accurately construct the inscribed circle.

Many examples of graph drawing software will allow you to directly construct angle bisectors and perpendicular lines, so it would be possible to approach the problem in the same way as on paper.

If this is not possible then we would need to think about the coordinate geometry of the problem, identifying the equation of the inscribed circle. We might choose to do this for a specific example before trying to find a general solution.

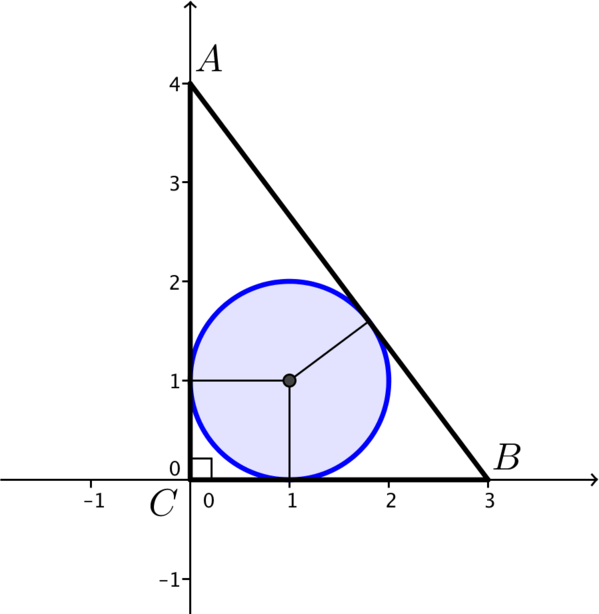
Triangle now has vertices A,B,C and three perpendiculars have been added that touch at the centre of the circle. Axes are also added

Can you find a right-angled triangle for which the inscribed circle has a radius of \(6\)?

Diagram	Description
	Using the fact that we have a square in the bottom left-hand corner of the outer triangle, we can label the length \(r\) on the outer triangle. We will label the sides of the outer triangle \(a\),\(b\) and \(c\) in the usual way.
	We can now label the other ‘portions’ of the perpendicular sides of the triangle \(a-r\) and \(b-r\) respectively. Because we know that we have pairs of congruent triangles, we can also label the two ‘portions’ of side length \(c\), the hypotenuse of the outer triangle. We can write down an expression for side-length \(c\): \[c = (a - r) + (b - r),\] which can be simplified to \[c = a + b - 2r.\]
	We have been asked about the specific case where \(r=6\) so we can substitute this into our diagram and our expression for side-length \(c\):\[c = a + b - 12.\]

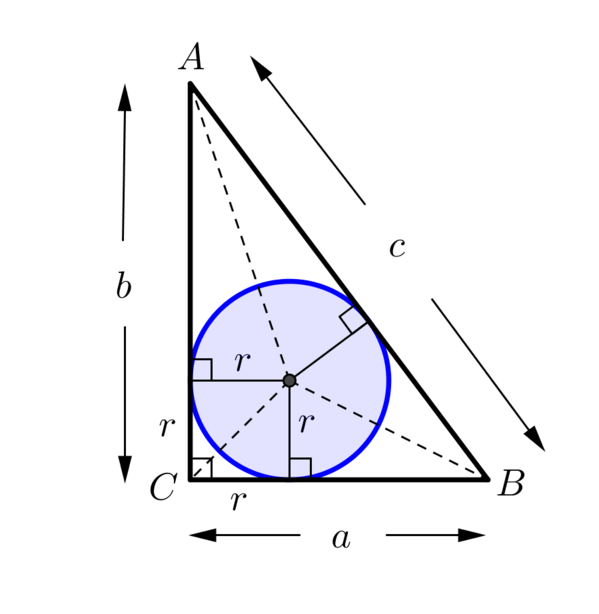
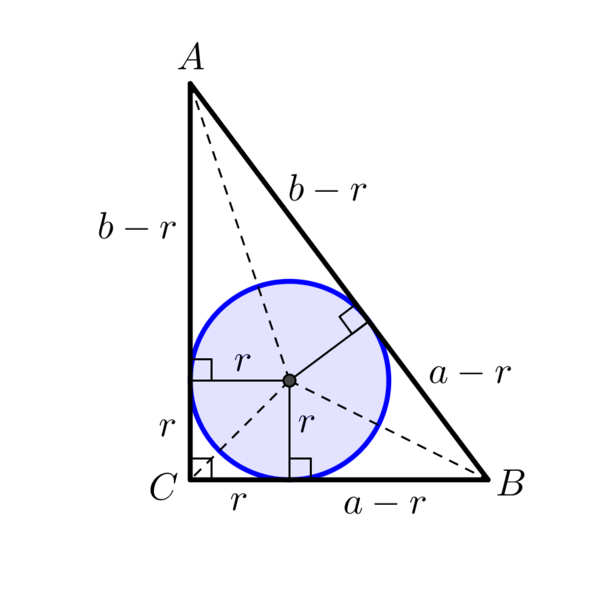
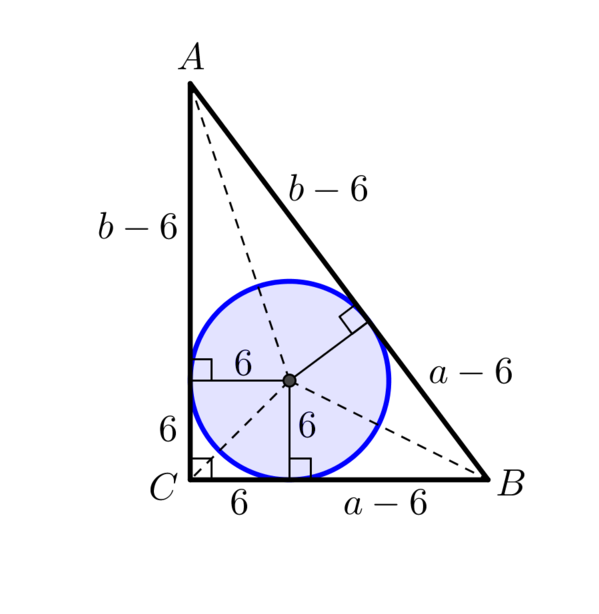
Now, we also require that outer triangle \(ABC\) is right-angled so we have the second condition that \[c^2 = a^2 + b^2.\]

If we substitute for \(c\) in the above equation we have \[(a+b-12)^2 = a^2 + b^2,\] which can be expanded to \[a^2 + b^2 + 144 + 2ab - 24a - 24b = a^2 + b^2,\] and simplified to \[72 + ab = 12(a + b).\]

We still have two unknown values in this equation, \(a\) and \(b\).

What happens if we assign a value to either \(a\) or \(b\) and use this to calculate the other?

Rearranging the above equation to make \(b\) the subject we have \[b = \frac{12(a - 6)}{a - 12}.\]

If we choose \(a=13\) then we obtain the following solution to the problem.

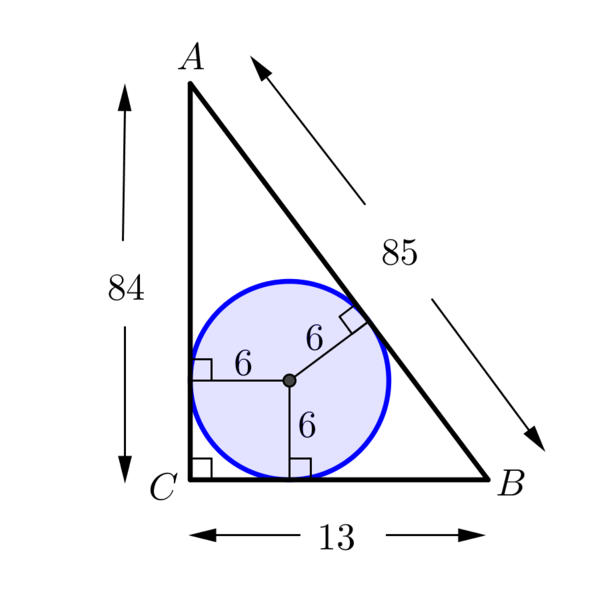
The circle is shown to have radius 6 and the triangle has side lengths 13, 85 and 84

Does it matter exactly which value we select for \(a\) or \(b\)?

Does the value we select need to be an integer?

Why might we have chosen \(a=13\)?

How does the denominator in our formula for \(b\) relate to the diagram, and what can it tell us about the values that we select?

Is your solution unique?

You may have some feeling for this already from the work done above.

You might like to experiment with the interactive diagram below in order to clarify your thinking.

What stays the same and what changes as you move point \(B\)?
What constraints are there on the base length of the triangle (line segment \(BC\))?
What constraints are there on the vertical height of the triangle (line segment \(CA\))?
How will your findings generalise to a right-angled triangle with an inscribed circle of radius \(r\)?

In our example above we chose the base length to be \(13\). It turns out that the other side lengths are also integer values (\(84\) and \(85\)). This is an example of a Pythagorean Triple.

How many integer solutions to this problem are there?

Download GeoGebra file

Previous Next

Thinking about Geometry

A perfect fit Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Solution

Tags

Bundles

Station

Lines

A perfect fit
Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource