Let \(a\), \(b\) and \(c\) be the lengths of the sides of a right-angled triangle, where \(c\) is the length of the hypotenuse. Then \(a^2 + b^2 = c^2\).
Here are some starting points for you to develop into proofs of Pythagoras’ theorem.
Which of these proofs do you find easiest to understand? Which do you find most convincing? Which give you the most understanding of why the theorem is true? Which would you choose to explain to someone else?
Approach 1
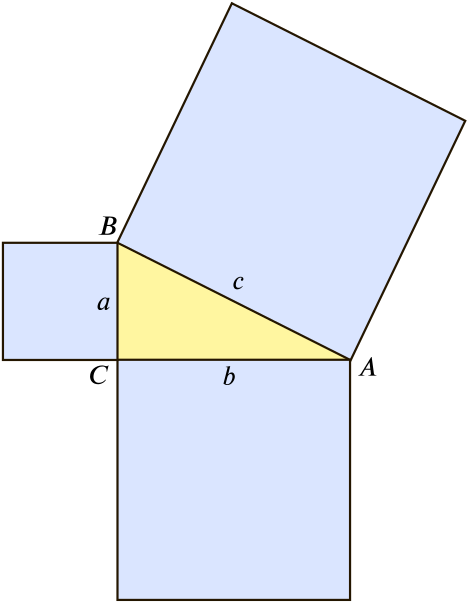
Take a right-angled triangle with vertices \(A\), \(B\) and \(C\) and side lengths \(a\), \(b\) and \(c\), as shown. (So \(c\) is the length of the hypotenuse, and \(C\) is the vertex with a right angle.)

Drop the perpendicular from \(C\) to \(AB\), and let \(X\) be the point where the perpendicular meets \(AB\).

What can you say about triangles \(ABC\), \(ACX\) and \(CBX\)?
Now use that to prove Pythagoras’ theorem.
Approach 2
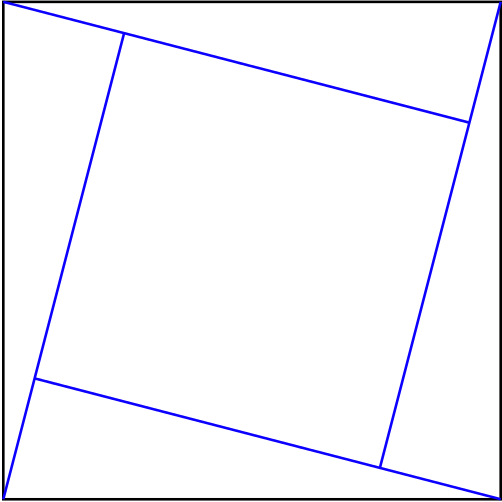
Draw a square, and mark a point a fixed distance from each corner. Join from each of these points to the nearer corner on the opposite side, as shown.

Cut along the edges marked below, to obtain five pieces.
Rearrange the pieces to make an L-shape as shown.
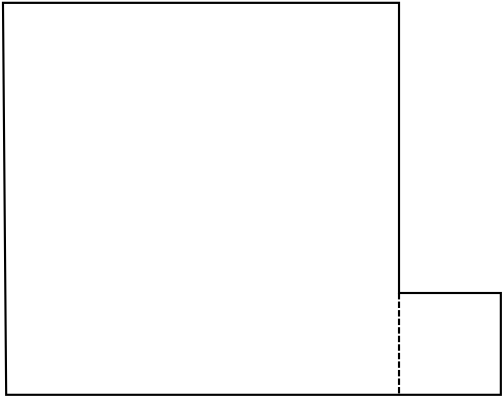
Now use that to prove Pythagoras’ theorem.
Approach 3

Rotate the trapezium around the centre of the longest side, to make a square. What is the area of the square? What is the area of the trapezium?
How else could you find an expression for the area of the trapezium?
Now use that to prove Pythagoras’ theorem.
Approach 4
Start with the triangle \(ABC\) and the squares constructed on its sides. Label the vertices of those squares as shown.
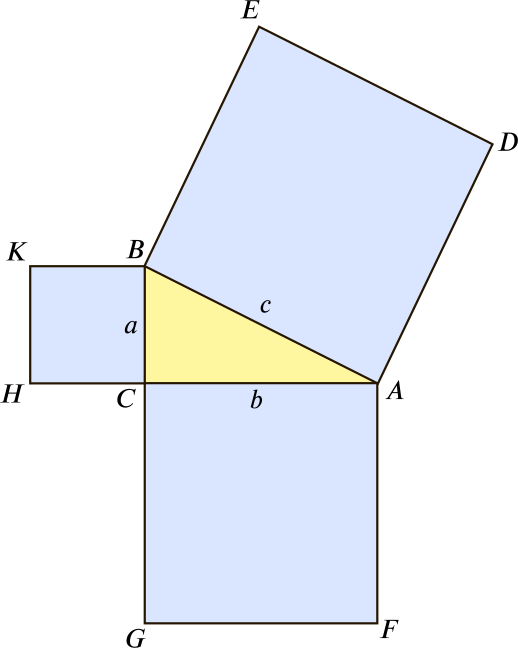
Draw line segment \(CL\) parallel to \(AD\) and with the same length as \(AD\), and draw in line segments \(LD\), \(CD\) and \(BF\).
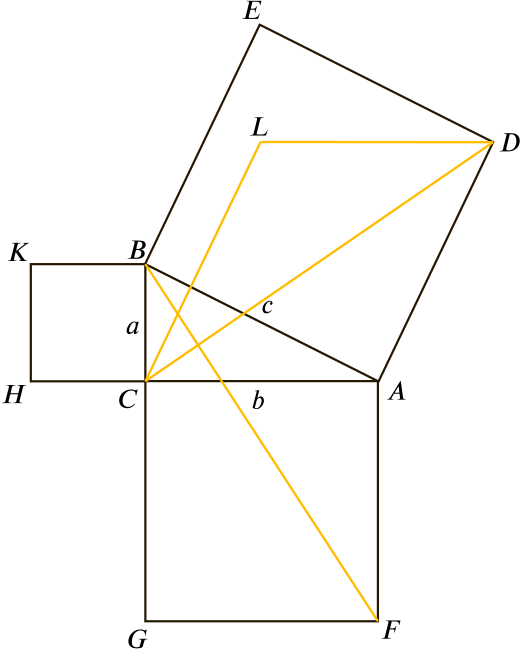
Show that triangle \(ADC\) is congruent to triangle \(ABF\).
Use that to show that the parallelogram \(ADLC\) has the same area as the square \(AFGC\).
Now do something similar to show that the parallelogram \(BCLE\) has the same area as the square \(BKHC\).
Now use that to prove Pythagoras’ theorem.
(You might like to watch this video. Can you see how it relates to Approach 4?)
Approach 5
Over to you! What other approaches can you come up with?

