A lune is the area left when part of a circle is cut off by another circle, as in the following problems. It is called a lune because it looks a bit like the moon.
In the following figure, two semicircles have been drawn, one on the side \(AB\) of the triangle, and the other on the side \(AC\) of the triangle (with centre \(O\)). What is the area of the blue (shaded) lune which is bounded by the two semicircles?
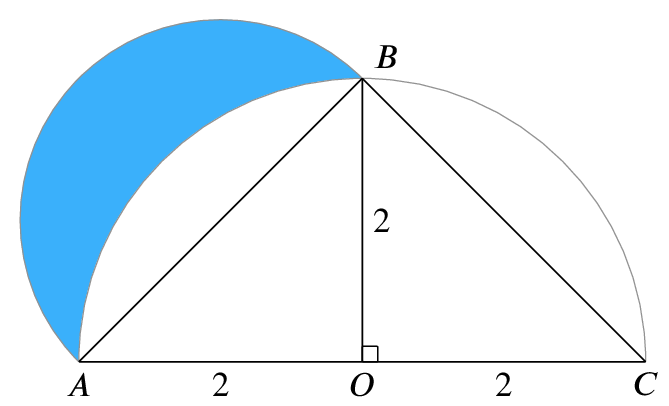
As a bonus, can you construct a square on the diagram with the same area as the blue lune, using only a straight edge (ruler) and compasses? This is called the quadrature (making into a square) of the lune.
In the following figure, three semicircles have been drawn, one on each of the sides of the right-angled \(6\)-\(8\)-\(10\) triangle. What is the total area of the two coloured (shaded) lunes in the drawing?
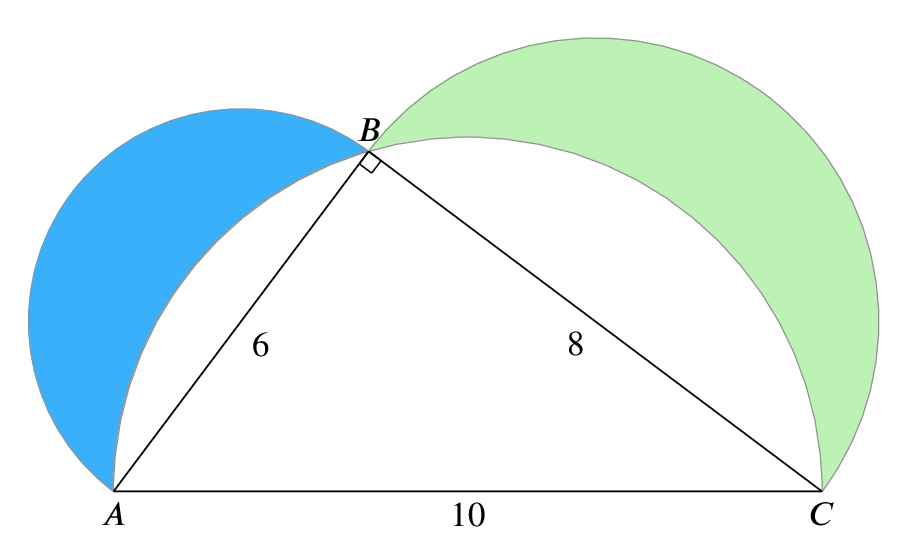
As a final (hard) challenge, can you find any other lunes associated with a circle which can be “squared”; that is, where it is possible to construct a square with the same area as the lune, using only the original circles, a straight edge and compasses? (For example, the lune in question 1 can be squared.)

