Can we use similar triangles to find this side?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

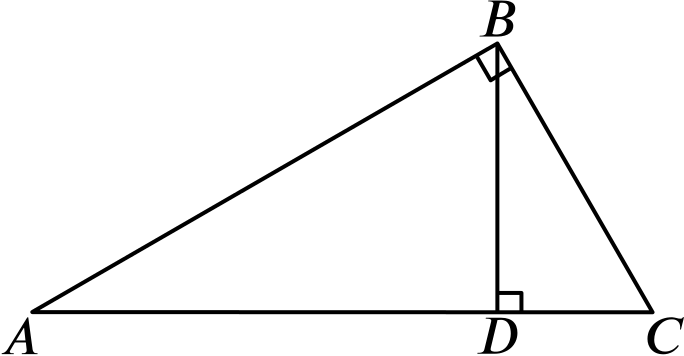
In the diagram, \(\widehat{ABC}=\widehat{BDC}=90^\circ\).

1. Write down an angle equal to \(\widehat{CBD}\).

The angle \(\widehat{BAD}\) is equal to \(\widehat{CBD}\).

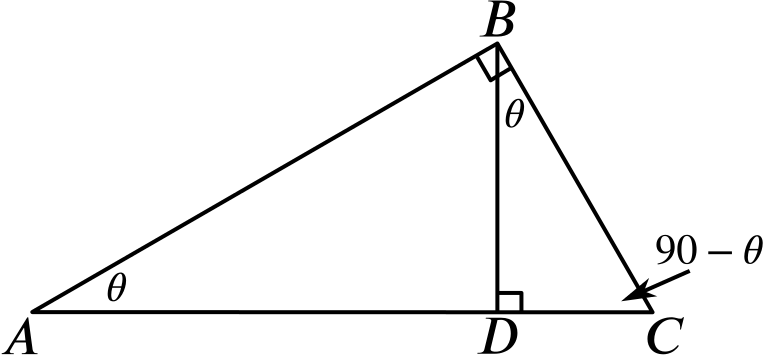
The angle \(\widehat{CBD}=90^\circ-\widehat{BCD}\), since the triangle \(BCD\) is right-angled.

Since the triangle \(ABC\) is right-angled, we also have that \(\widehat{BAD}=90^\circ-\widehat{BCD}=\widehat{CBD}\).

2. Given that \(AC= \quantity{10}{cm}\) and \(BC=\quantity{7}{cm}\), use similar triangles to calculate \(CD\).

The two right-angled triangles \(BCD\) and \(ABC\) are similar, since their angles are equal.

So the ratios of the corresponding side lengths are equal, giving \[ \frac{CD}{7}=\frac{7}{10}, \] and so \(CD=\dfrac{49}{10}=\quantity{4.9}{cm}\).