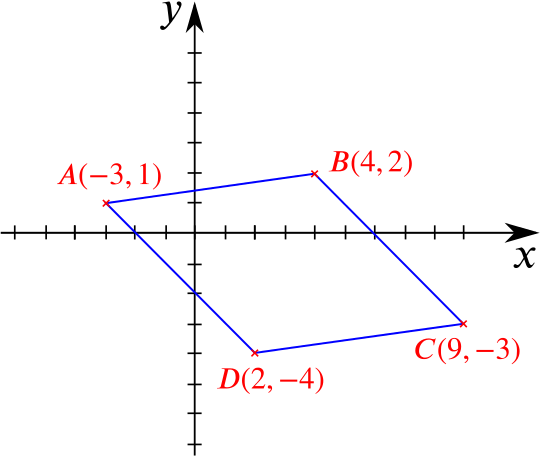
Draw a diagram showing points \(A(-3,1)\), \(B(4,2)\), \(C(9,-3)\), \(D(2,-4)\).
- For the figure \(ABCD\) state and prove a fact (or facts) sufficient to ensure that it is a parallelogram.
Drawing a diagram is a good idea.
Approach 1
A parallelogram is a quadrilateral where opposite sides have equal lengths, so all we have to show is that \(AB=CD\) and \(AD=BC\).
The length of the sides can be calculated with the use of Pythagoras’ theorem by constructing right triangles between the points. We then find
\[\begin{align*} AB &= \sqrt{(-3-4)^2+(1-2)^2} &=\sqrt{50},\\ CD &= \sqrt{(9-2)^2+(-3+4)^2} &=\sqrt{50},\\ AD &= \sqrt{(-3-2)^2+(1+4)^2} &=\sqrt{50},\\ BC &= \sqrt{(4-9)^2+(2+3)^2} &=\sqrt{50}. \end{align*}\]This certainly satisfies \(AB=CD\) and \(AD=BC\). The figure therefore is a parallelogram.
Approach 2
A quadrilateral is a parallelogram if and only if its diagonals bisect each other. Midpoint(\(AC\)) = (\(3,-1\)) = Midpoint (\(BD\)), so \(ABCD\) must be a parallelogram.
- State and prove an additional fact sufficient to ensure that \(ABCD\) is a rhombus.
A rhombus is a quadrilateral with four equal sides. We’ve already calculated all four side lengths, and they’re equal, so \(ABCD\) must be a rhombus.
- Prove that \(ABCD\) is not a square.
Approach 1
If we can prove that any of the angles inside the figure is not a right angle, then this would show that \(ABCD\) isn’t a square.
The angle at \(C\) is a right angle if and only if \(AC^2 = AD^2 + CD^2\). In fact, we find
\[\begin{align*} AC^2 &= (-3-9)^2+(1+3)^2 &= 160,\\ AD^2 + CD^2 &= 50 + 50 &= 100. \end{align*}\]The figure is therefore not a square.
Approach 2
A square is a rhombus where diagonals have equal lengths. So all we have to consider is whether \(AC=BD\). A short calculation reveals
\[\begin{align*} AC &= \sqrt{(-3-9)^2+(1+3)^2} &= \sqrt{160},\\ BD &= \sqrt{(4-2)^2+(2+4)^2} &= \sqrt{40}. \end{align*}\]Once again, we see that \(ABCD\) is not a square.
Approach 3
Gradient(\(AB\)) = \(1/7\), Gradient(\(BC\)) = \(-1\), so their product is not \(-1\). Thus the angle at \(B\) is not a right angle, and \(ABCD\) is not a square.

