State the theorem of Pythagoras concerning the three sides of a right-angled triangle.
Pythagoras’s theorem states that, if we are given a right-angled triangle with sides \(a, b\) and \(c\), where \(c\) is the side opposite the right angle, then \[ a^2 + b^2 = c^2. \]
In fact the converse to this is true also, so we can say that a triangle with sides \(a, b\) and \(c\), where \(c\) is the longest side, is right-angled if and only if \(a^2 + b^2 = c^2.\)

The diagram shows an isosceles triangle \(ABC\) right-angled at \(B\). Semicircles \(S_1\) and \(S_2\) are drawn on \(AB\) and \(AC\) as diameter, as shown.
- Explain why \(S_2\) passes through \(B\).
We know the circle theorem, ‘The angle in a semicircle is a right angle’. We are given here that \(AC\) is a diameter of \(S_2\), and that \(B\) is a right angle. If \(B\) is inside \(S_2\), then we can find a point \(B'\) on \(S_2\) where the angle \(AB'C\) is less than a right angle, which is a contradiction.
Similarly, if \(B\) is outside \(S_2\), then we can find a point \(B'\) on \(S_2\) where the angle \(AB'C\) is more than a right angle, which is also a contradiction. Thus \(B\) is on \(S_2\).
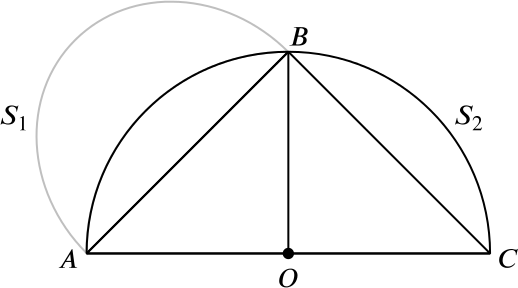
Or alternatively we can say that \(AB = BC, \quad AO = OC\) (where \(O\) is the centre of \(S_2\)), and angle \(BAO\) equals angle \(BCO\), and so the triangles \(ABO\) and \(BCO\) are congruent right-angled isosceles triangles.
This means \(AO = BO\) = radius of \(S_2\), and \(B\) must be on the semicircle.
- If \(AB = \quantity{2x}{cm}\), show that the area shaded vertically is \(\quantity{\tfrac{1}{2}(\pi - 2)x^2}{cm^2}\).
We’ll begin with the following two diagrams.


We can write \[ \text{area of the vertically-shaded region} = \text{area of the blue region} - \text{area of the red region}. \]
The blue region is a quarter of the area of the circle that includes \(S_2\). We know that \(\triangle AOB\) is an isosceles triangle, with \(AB\) as the hypotenuse. Since \(AB\) has length \(2x\), and since \(OA=OB=r\), where \(r\) is the radius of \(S_2\), by Pythagoras’ theorem we know that \[ (2x)^2 = OA^2 + OB^2 = 2r^2, \] which implies that \(r^2 = 2x^2\). Thus \[\begin{align*} \text{area of the blue region} &= \frac{1}{4} \times \text{area of the circle} \\ &= \frac{1}{4} \times \pi r^2\\ &= \frac{\pi x^2}{2}. \end{align*}\] The red region is an isosceles, right-angled triangle, so \[\begin{align*} \text{area of the red region} &= \frac{1}{2} \times \text{base} \times \text{height} \\ &= \frac{1}{2} r^2 \\ &= x^2. \end{align*}\] So we have \[\begin{align*} \text{area of the vertically-shaded region} &= \frac{\pi x^2}{2} - x^2 \\ &= \quantity{\frac{1}{2} \left( \pi - 2 \right) x^2}{cm^2}. \end{align*}\]- Prove that the area shaded horizontally is half the area of the triangle \(ABC\).
It is easy to see the area of \(\triangle ACB\) is \(\quantity{2x^2}{cm^2}\), which is twice the area of the horizontally-shaded region.

