The sum of the interior angles of a polygon with \(n\) sides is \((2n-4)\) right angles. Deduce that each interior angle of a regular polygon is \(\left( 2 - \dfrac{4}{n} \right)\) right angles.
A regular polygon with \(n\) sides has \(n\) interior angles, with all of these angles being equal. Thus, each interior angle is \[ \frac{1}{n} \left( 2n - 4 \right) = 2 - \frac{4}{n} \] right angles.
Three regular polygons, two having \(n\) sides and one having \(p\) sides, fit together exactly at a common vertex, as shown:
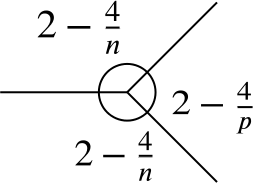
By using the fact that the sum of the three angles shown is four right angles, prove that \[ \frac{4}{n} + \frac{2}{p} = 1. \]
as required.
Show that this formula can be rearranged into the form \[ p = \frac{2n}{n-4}. \]
By inserting into this formula various values of \(n\), list all the pairs of positive integers \((n,p)\) for which \(n < 12\) which satisfy this equation.
As \(n\) is a positive integer, in order for \(p\) to be positive we require that \(n > 4\). By substituting values in, we have the following table.
| \(n\) | \(p = \dfrac{2n}{n-4}\) |
|---|---|
| \(5\) | \(10\) |
| \(6\) | \(6\) |
| \(7\) | \(\dfrac{14}{3}\) |
| \(8\) | \(4\) |
| \(9\) | \(\dfrac{18}{5}\) |
| \(10\) | \(\dfrac{20}{6}\) |
| \(11\) | \(\dfrac{22}{7}\) |
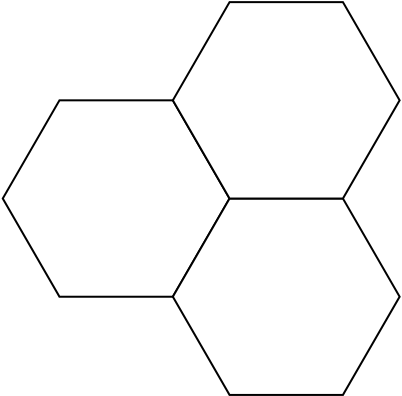
Thus, the suitable pairs $(n,p) $are \((5,10)\), \((6,6)\) and \((8,4)\).
We could note that \((12,3)\) will also work as a pair, and since \(p \geq 3\), no other pairs are possible.
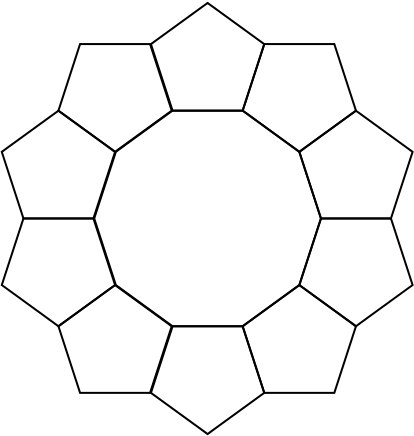
By means of a sketch, interpret one of these solutions where \(n\) and \(p\) are different in terms of three regular polygons meeting at a common vertex.
We will consider the neater of the two cases: \((8,4)\), which is shown below. (In fact, this arrangement will tessellate, that is, tile the entire plane. This is termed the truncated square tiling, and is one of the semi-regular tessellations.)