The answers we found were approximate, as they relied on estimating through a scale drawing. The lengths and areas discussed can, in fact, be calculated exactly (although not easily!) through trigonometry.
Suppose that we have a the following graph, where \(0 < \alpha < 90^\circ\), \(0 < \beta < 90^\circ\), and \(A = (0,0)\).
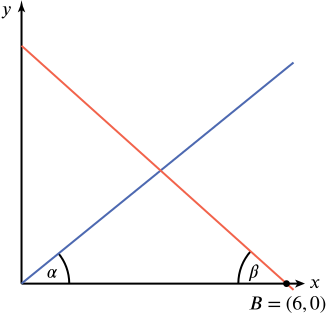
The line through the origin has equation \(y = (\tan \alpha) x\), while the second has equation \(y = -(\tan \beta) x - 6 \tan \beta\).
Solving these simultaneously, we find that the point of intersection between the lines has coordinates \[ \left( \frac{6 \tan \beta}{\tan \alpha + \tan \beta}, \frac{6 \tan \alpha \tan \beta}{\tan \alpha + \tan \beta} \right). \]
In the situation in the question, we have the following values for \(\alpha\) and \(\beta\).
| Vertex | \(\alpha\) | \(\beta\) |
|---|---|---|
| \(C\) | \(25^\circ\) | \(60^\circ\) |
| \(D\) | \(25^\circ\) | \(65^\circ\) |
| \(E\) | \(30^\circ\) | \(65^\circ\) |
| \(F\) | \(30^\circ\) | \(60^\circ\) |
We can therefore calculate the coordinates of \(C\), \(D\), \(E\), and \(F\) by plugging these values into the formula above; let these be denoted by \((C_x,C_y)\), \((D_x,D_y)\), \((E_x,E_y)\), and \((F_x,F_y)\), respectively.
Closest point
This is the length of \(BD\). Thus, it equals \[ \quantity{\sqrt{ \left(6 - \frac{6 \tan 65^\circ}{\tan 25^\circ + \tan 65^\circ}\right)^2 + \left(\frac{6 \tan 65^\circ \tan 25^\circ}{\tan 25^\circ + \tan 65^\circ}\right)^2 }}{km} = \quantity{2.53570957\!\ldots}{km} \approx \quantity{2.54}{km} \] which is remarkably close to the estimate.
Furthest point
This is whichever is smaller of \(BE\) and \(BF\). The length of \(BE\) is \[ \quantity{\sqrt{ \left(6 - \frac{6 \tan 65^\circ}{\tan 30^\circ + \tan 65^\circ}\right)^2 + \left(\frac{6 \tan 65^\circ \tan 30^\circ}{\tan 30^\circ + \tan 65^\circ}\right)^2 }}{km} = \quantity{3.01145951\!\ldots}{km} \approx \quantity{3.01}{km} \] while the length of \(BF\) is \[ \quantity{\sqrt{ \left(6 - \frac{6 \tan 60^\circ}{\tan 30^\circ + \tan 60^\circ} \right)^2 + \left( \frac{6 \tan 60^\circ \tan 30^\circ}{\tan 30^\circ + \tan 60^\circ} \right) }}{km} = \quantity{3}{km} \] exactly. Thus, \(BE\) is in fact slightly longer than \(BF\), and the greatest length is approximately \(\quantity{3.01}{km}\).
Area of \(CDEF\)
The area of a convex quadrilateral \(CDEF\), whose vertices are traversed in an anti-clockwise direction, can be written as \[ \frac{1}{2} \cdot \text{length of $CE$} \cdot \text{length of $DF$} \cdot \sin \left( \text{angle between $CE$ and $DF$} \right). \]
As we are taking the sine of the angle, it does not matter whether we take the acute or obtuse angle between the two lines.
By Pythagoras’s theorem, the lengths of \(CE\) and \(DF\) are \[ \sqrt{(C_x - E_x)^2 + (C_y - E_y)^2} \quad\text{and}\quad \sqrt{(D_x - F_x)^2 + (D_y - F_y)^2} \] respectively. As for the angle, this is \[ \tan^{-1} \left( \frac{E_y - C_y}{E_x - C_x}\right) + \tan^{-1} \left( \frac{F_y - D_y}{F_x - D_x} \right). \] In our case, since \(E_x = C_x\), and given that this first summand is to be interpreted as the angle between \(CE\) and the \(x\)-axis, we will take \[ \tan^{-1} \left( \frac{E_y - C_y}{E_x - C_x} \right) = 90^\circ. \]
We therefore have an exact, if quite horrendously messy, value for the exact area of the shaded region. Numerically, this value is \[\quantity{0.137244709\!\ldots}{sq. km}.,\] which is a fair amount more than our estimate using the graph paper.

