\(A\) and \(B\) are two lifeboat stations on a North-facing coast, \(B\) being \(\quantity{6}{km}\) due East of \(A\). A distress call from a ship is received simultaneously at both stations. The bearing of the call from \(A\) is measured to lie between \(060^\circ\) and \(065^\circ\). The bearing of the call from \(B\) is measured to lie between \(330^\circ\) and \(335^\circ\). By means of a scale drawing on squared paper find as accurately as possible
- the least and greatest possible distances of the distressed ship from \(B\), and
We will begin with a diagram of the situation.
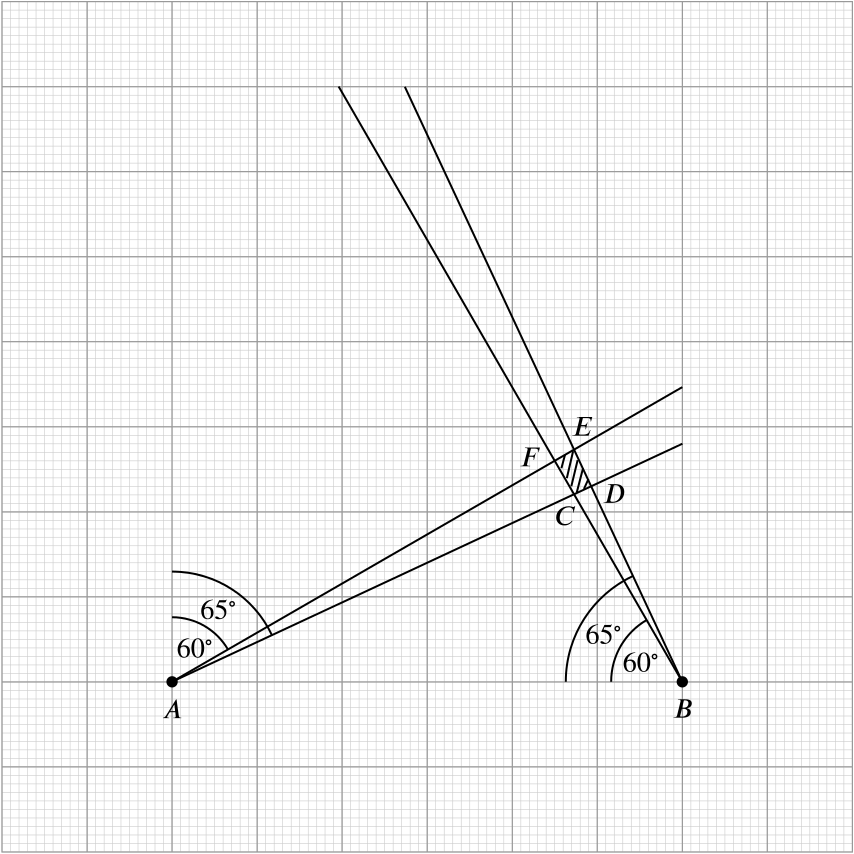
In this diagram, successive major gridlines are a kilometer apart and successive minor gridlines are a tenth of a kilometer apart. The dotted region denotes the coast, and the hatched region denotes the region in which the source of the distress call originated.
For the first part of the question, we are to find (using the graph paper) the distance from \(B\) to the closest and furthest points in the hatched region.
Closest point
The nearest point to \(B\) lies on the southernmost edge of the hatched region (i.e., that which contains the segment \(AC\)).
This is because, for any point \(P\) in the hatched region, the line segment \(BP\) has to pass through the line segment \(CD\), and this point of intersection is closer to \(B\) than \(P\).
Since this line and \(BD\) are perpendicular to one another, and since \(D\) lies on the line, the closest point on the line to \(B\) is the point \(D\).
By examining the diagram, the horizontal distance from \(B\) to \(D\) is approximately \(\quantity{1.1}{km}\), while the vertical distance is approximately \(\quantity{2.3}{km}\) and so, by Pythagoras’s theorem, the approximate distance is \[ \quantity{\sqrt{(2.3)^2 + (1.1)^2}}{km} = \quantity{2.54950975\!\ldots}{km} \approx \quantity{2.55}{km}. \] (This can also be checked by using a ruler on the diagram.)
Furthest point
Similarly to the previous case, the furthest point must lie on the northernmost edge of the hatched region.
For any point \(P\) in the hatched region, if we draw the ray originating at \(B\) and passing through \(P\), then this ray has to pass through the line segment \(EF\); this point of intersection is more distant from \(B\) than \(P\).
In fact, the most distant point from \(B\) in the hatched region must be \(E\) or \(F\).
If \(BE\) is longer than \(BF\), we can draw a disc centred at \(B\) with \(DE\) as a radius. As \(E\) and \(F\) fall within the disc, the line segment \(EF\) falls entirely within the disc (as the disc is convex), so no point within \(EF\) can be closer to \(B\) than \(E\) is.
Since we can swap \(E\) and \(F\) in this argument, the most distant point from \(B\) in the hatched region must be one of \(E\) or \(F\).
As the horizontal distance between \(B\) and \(E\) is approximately \(\quantity{1.3}{km}\) and the vertical distance is approximately \(\quantity{2.7}{km}\), by Pythagoras’s theorem the length of \(BE\) is approximately equal to \[ \quantity{\sqrt{(1.3)^2 + (2.7)^2}}{km} = \quantity{2.99666481\!\ldots}{km} \approx \quantity{3.00}{km}. \]
Similarly, the length of \(BF\) is approximately equal to \[ \quantity{\sqrt{(1.5)^2 + (2.6)^2}}{km} = \quantity{3.00166620\!\ldots}{km} \approx \quantity{3.00}{km}. \]
Thus, while \(BF\) appears to be slightly longer than \(BE\), both are approximately \(\quantity{3.00}{km}\) in length.
(Again, this can also be checked by using a ruler on the diagram.)
- the area that may need to be searched, giving your answer in square kilometers to two significant figures.
As there are (when considering partial squares!) approximately ten full \(\quantity{0.1}{km}\)-by-\(\quantity{0.1}{km}\) squares within the hatched region, the area of the hatched region is approximately \(\quantity{0.10}{sq. km}\).

