A toy pool table is \(\quantity{6}{feet}\) long and \(\quantity{3}{feet}\) wide. It has pockets at each of the four corners \(P\), \(Q\), \(R\) and \(S\). When a ball hits a side of the table, it bounces off the side at the same angle as it hit that side. A ball, initially 1 foot to the left of the pocket \(P\), is hit from the side \(SP\) towards the side \(PQ\) as shown.
How many feet from \(P\) does the ball hit side \(PQ\) if it lands in pocket \(S\) after two bounces?
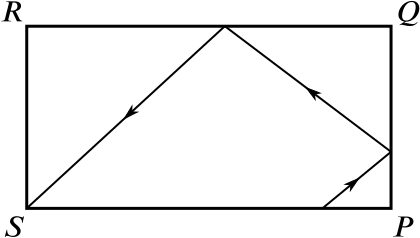
Method 1
Look at the picture:
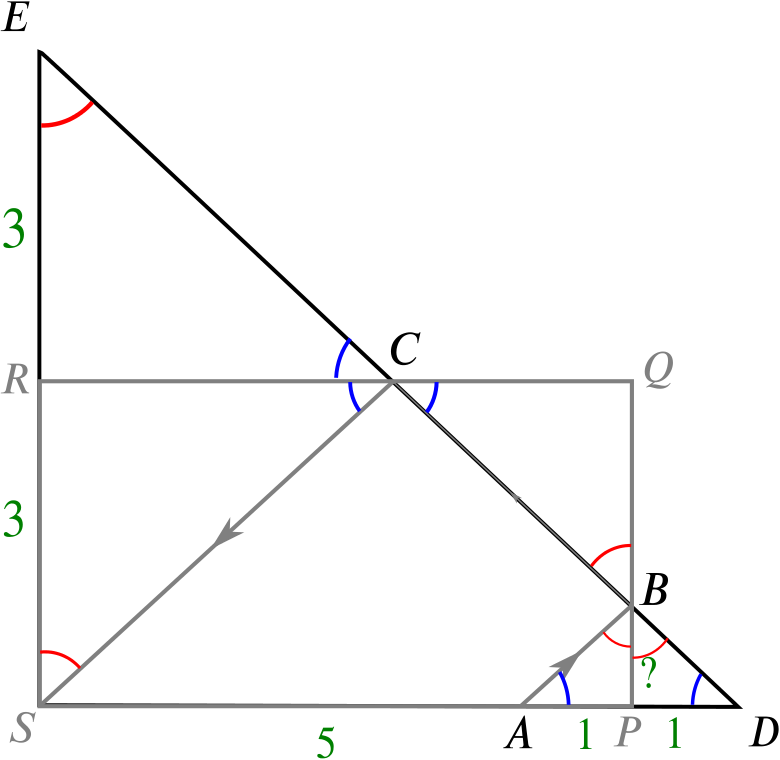
Point \(D\) is given by the point \(A\), where the ball is hit, reflected in the line \(PQ\) while point \(E\) is point \(S\) reflected in \(RQ\), and the ball takes the path \(A\to B\to C\to S\).
We know that all of the red angles (the three angles at B) are the same, since the ball leaves the side of the table by the same angle it hits it (angle \(CBQ\)), or because the triangles mirror one another (angle \(PBD\)), and similarly for the blue angles (the three angles at C). Notice that the red angle and blue angle are related: they must add up to \(90^\circ\). Let’s call the blue angles \(\beta\).
Remember that the angles of a triangle add up to \(180^\circ\).
We can work out that the points \(E, C, B\) and \(D\) all lie on a straight line: angle \(SCB=180^\circ-2\beta\) so \[\text{angle }ECB=\beta+\beta+SCB=2\beta+180^\circ-2\beta=180^\circ.\] A similar calculation for the red angles shows that angle \(CBD\) is also \(180^\circ\). So \(ESD\) is a triangle, and furthermore, since \(ESD\) and \(BPD\) are both right-angled triangles which share an angle (\(BDP\)), they are similar.
For two similar triangles, the ratios of the sides are the same:
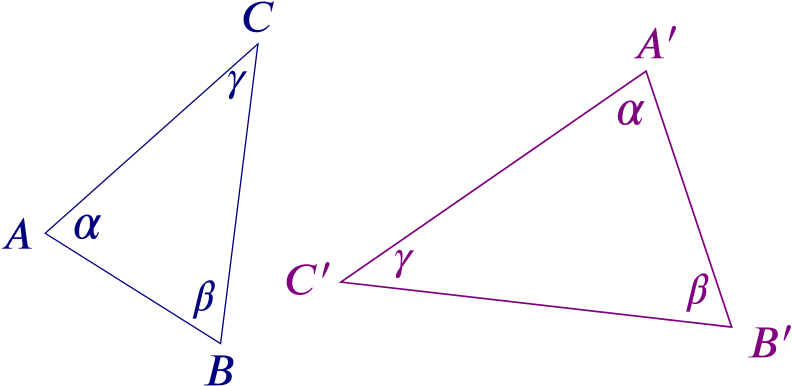
\[\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'}.\]
We can now calculate the length of \(BP\):
\[\begin{align*} \frac{BP}{PD}&=\frac{ES}{SD}, \\ \frac{BP}{1}&=\frac{6}{7}, \\ BP&=\frac{6}{7}. \end{align*}\]Method 2
The solution above might be a bit difficult to spot, since it involves the idea about reflecting the path outside the table.
We’ll now give a different solution using the triangles we can already see, using simultaneous equations to find the unknown length.
Consider the picture below:
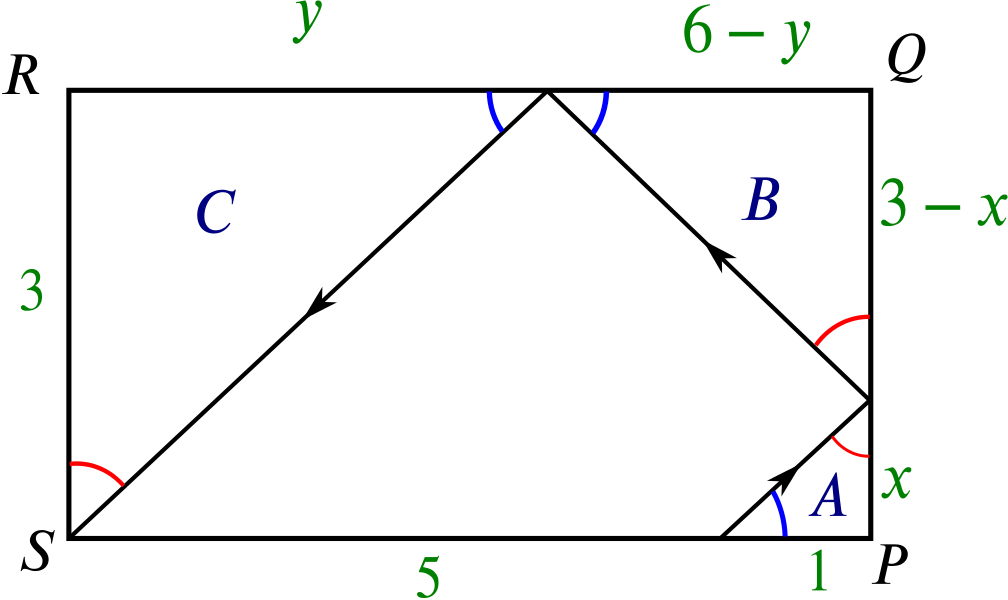
The triangles \(A\), \(B\) and \(C\) are all similar since the red angles and blue angles are the same. We know this because we are told that the ball bounces off the side of the table at the same angle at which it hits it, and also since we know the two non-right angles in each triangle must add up to \(90^{\circ}\). We can derive an equation for each pair of triangles: \[A \;\& \; B: \quad \frac{x}{1}=\frac{3-x}{6-y},\] \[A \;\& \; C: \quad \frac{x}{1}=\frac{3}{y},\] \[B\;\& \; C: \quad \frac{3}{y}=\frac{3-x}{6-y}.\]
(Note that these equations are not independent; the last is given by the first two.)
Rearranging the equation from triangles \(A\) and \(B\) we see that \[6x - xy = 3 - x,\] so \[xy=6x+x-3=7x-3.\]
We leave it in this form because one of our other equations after rearranging will have an \(xy\) on one side and a constant on the other.
The equation from triangle \(A\) and \(C\) says \(xy=3\). So we can see that \[7x-3=xy=3.\] Now we have an equation that’s easy to solve: \[7x-3=3 \implies x=\frac{6}{7}.\]
We can use this to find \(y\), and then substitute these values back in to the equation from \(B\) and \(C\) to check we have done everything right and really do have a solution.

