A toy pool table is \(\quantity{6}{feet}\) long and \(\quantity{3}{feet}\) wide. It has pockets at each of the four corners \(P\), \(Q\), \(R\) and \(S\). When a ball hits a side of the table, it bounces off the side at the same angle as it hit that side. A ball, initially 1 foot to the left of the pocket \(P\), is hit from the side \(SP\) towards the side \(PQ\) as shown.
How many feet from \(P\) does the ball hit side \(PQ\) if it lands in pocket \(S\) after two bounces?
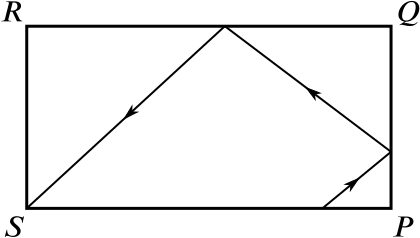
Can we draw a picture?
What happens if we reflect parts of the ball’s journey in the sides of the table?
Which angles are the same in our diagrams?
Can we work out the lengths of sides using what we know about similar triangles?

