A square has each side of length \(6x\) units. A circle is drawn with its centre at the centre of the square to intercept a length of \(2x\) units on each side of the square. Prove that the ratio of the area of the circle to the area of the square is \(5\pi:18\).
The square and circle look like this:
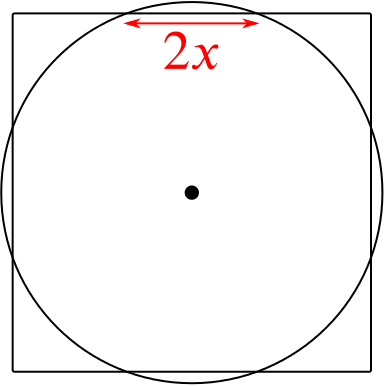
We know that the area of the square is \(6x\times 6x=36x^2\). To find the radius, \(r\), of the circle we use the following triangle:

The hypotenuse of the triangle is \(r\), one side has length \(x\) and the other has length \(3x\). Therefore, \[ r^2=x^2+(3x)^2=10x^2. \] So the area of the circle is \(\pi r^2=10x^2\pi\).
So the ratio of the area of the circle to the area of the square is \(10x^2\pi:36x^2\), which is equivalent to \(5\pi:18\), as required.
You might have noticed that the \(x\) doesn’t appear in our answer. Why is this? Could we have solved this without using \(x\)?

