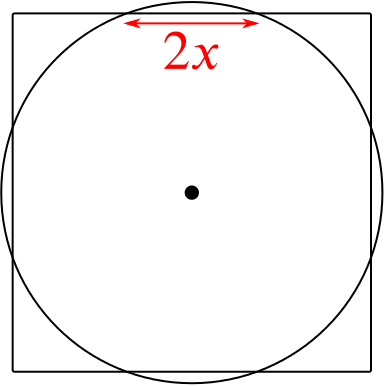
A square has each side of length \(6x\) units. A circle is drawn with its centre at the centre of the square to intercept a length of \(2x\) units on each side of the square. Prove that the ratio of the area of the circle to the area of the square is \(5\pi:18\).
What do you think it means for the circle to “intercept a length of \(2x\) units on each side of the square”?
Could we draw a diagram to make it clearer?
If you’re still unsure, click to reveal how we’ve drawn it.
Can you spot a right-angled triangle in your diagram that will help you to find the radius of the circle?