Prove that the internal bisector of an angle of a triangle divides the opposite side in the ratio of the lengths of the containing sides.
Can we draw a stetch that includes everything we know? Can we somehow apply the sine or cosine rule to the problem?
In a triangle \(ABC\), \(I\) is the incentre, \(H\) the orthocentre, and \(O\) the circumcentre. Prove that \(AI\) bisects \(\angle OAH\).
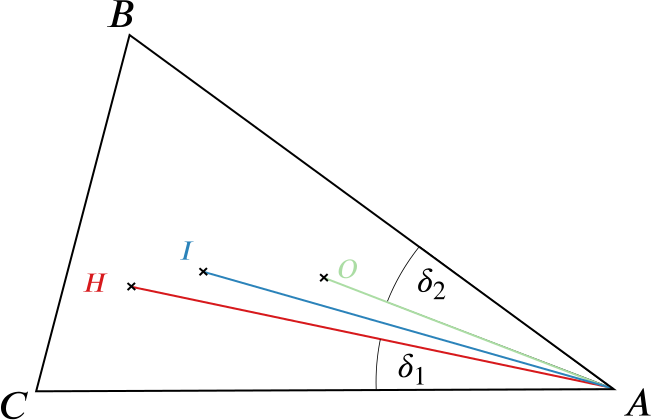
Can we show these two angles are equal?
Hence, or otherwise, prove that if \(O\), \(H\) and \(I\) are collinear the triangle must be isosceles.
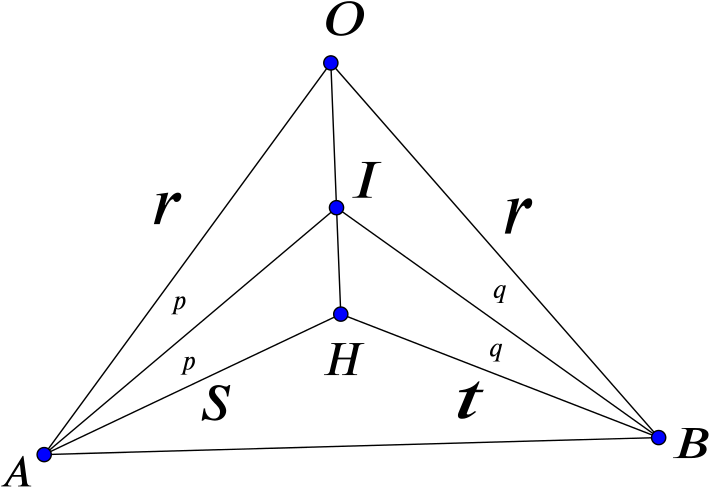
Why are the two lengths labelled \(r\) equal here? Can we use our results from the first and second parts?

