Prove that the internal bisector of an angle of a triangle divides the opposite side in the ratio of the lengths of the containing sides.
Let’s start with a sketch.
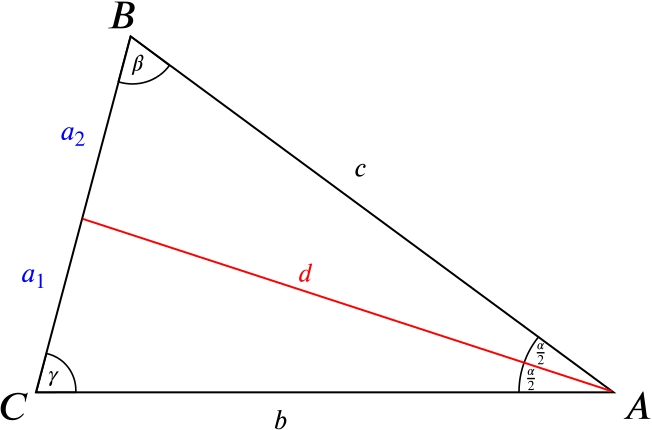
All we have to do is prove the statement
\[\begin{equation} \label{eq:1} \frac{b}{c}=\frac{a_1}{a_2}. \end{equation}\]First we can apply the sine rule to the two smaller triangles created by the line \(d\), giving
\[\begin{align*} I:&& \frac{d}{\sin \gamma} &= \frac{a_1}{\sin \frac{\alpha}{2}},&&\quad\\ II:&& \frac{d}{\sin \beta} &= \frac{a_2}{\sin \frac{\alpha}{2}}.\\ \end{align*}\]Dividing \(I\) by \(II\) leads to
\[\begin{equation} \label{eq:2} \frac{\sin \beta}{\sin \gamma} = \frac{a_1}{a_2}. \end{equation}\]Our last step is to apply the sine rule on the big triangle \(ABC\), giving
\[\begin{equation} \label{eq:3} \frac{\sin \beta}{\sin \gamma} = \frac{b}{c}. \end{equation}\]Combining the equations \(\eqref{eq:2}\) and \(\eqref{eq:3}\) finally proves \(\eqref{eq:1}\).
In a triangle \(ABC\), \(I\) is the incentre, \(H\) the orthocentre, and \(O\) the circumcentre. Prove that \(AI\) bisects \(\angle OAH\).
Let’s sketch a triangle \(ABC\) and construct the points \(I\), \(H\) and \(O\) in it. This gives
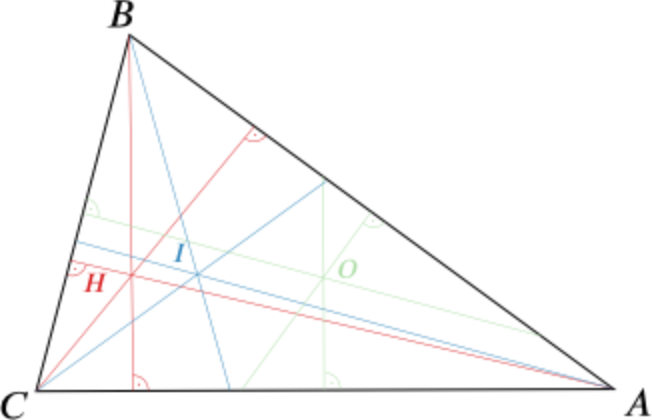
To simplify the picture, we’ll leave out all lines not connected to \(A\). We have to show that the two angles \(\angle HAI\) and \(\angle IAO\) are equal. Since we know that \(AI\) is bisecting the angle in \(A\), this comes down to proving \(\delta_1 = \delta_2\), for the two angles shown below.
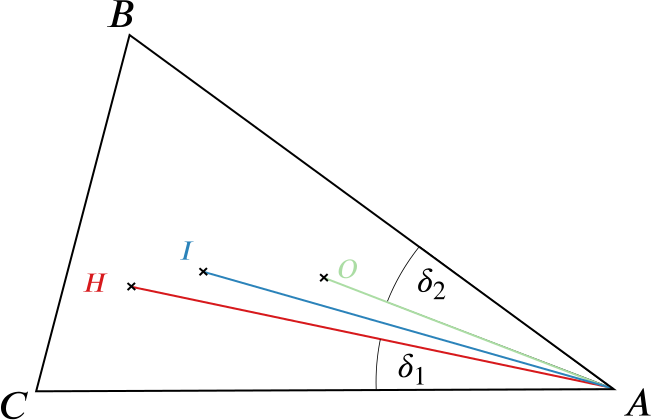
We start by taking a look at a simplified picture of the triangle and its orthocentre.

To define \(\delta_2\), we sketch the triangle and its circumcentre.
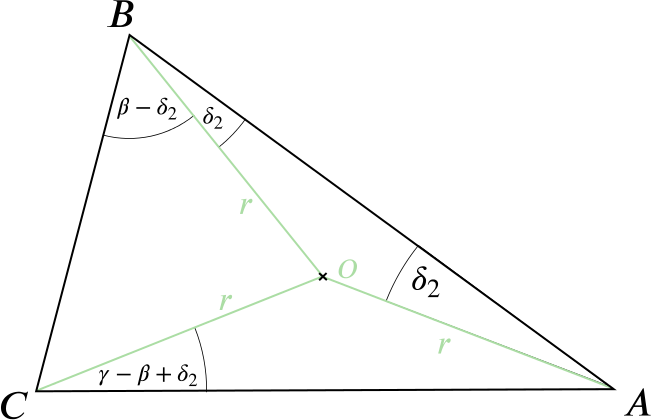
Since we know that the distance from the circumcentre to each of the corner points is equal, \(ABO\) is an isosceles triangle and \(\angle ABO\) equals \(\delta_2\). Hence \(\angle OBC = \beta - \delta_2 = \angle OCB\), which leads to \(\angle CAO = \gamma - \beta + \delta_2\).
Remembering that the full angle in \(A\) is \(\alpha\), and that we have \(\alpha + \beta + \gamma = \pi\), we can write
\[\begin{align} \label{eq:5} \alpha &= \delta_2 + \gamma - \beta + \delta_2\\ \nonumber \alpha + \beta + \gamma &= 2 \delta_2 + 2\gamma\\ \nonumber \delta_2 &= \frac{\pi}{2} - \gamma. \end{align}\]Comparing equation \(\eqref{eq:4}\) with equation \(\eqref{eq:5}\) proves \(AI\) does indeed bisect \(\angle OAH\).
Hence, or otherwise, prove that if \(O\), \(H\) and \(I\) are collinear the triangle must be isosceles.
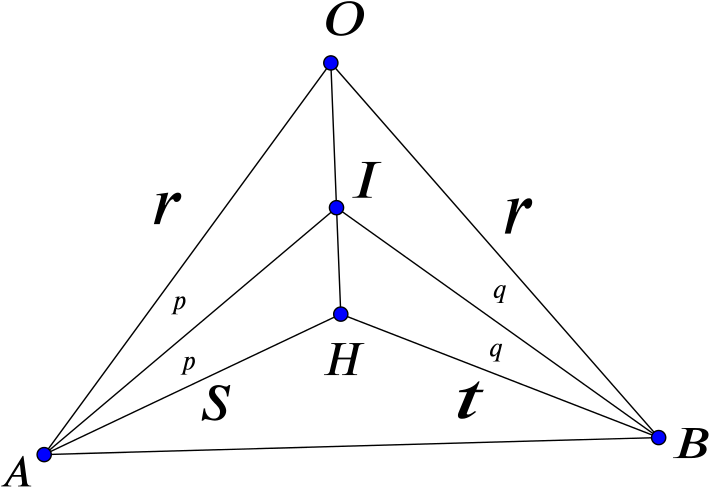
Suppose that \(H, I\) and \(O\) are collinear. Then \(A, B\), and \(C\) cannot all lie on one side of \(OIH\), since \(I\) is inside the triangle.
Suppose then that \(A\) and \(B\) lie on opposite sides of the line \(OIH\). We have \(OA = OB = r\), since \(O\) is the circumcentre of the triangle \(ABC\).
We have that \(IA\) bisects the angle \(OAH\), from our work above. Similarly \(IB\) bisects the angle \(OBH\).
From the diagram and our first result above, \(\dfrac{x}{y} = \dfrac{r}{s} = \dfrac{r}{t}\), and so \(s = t\).
This means that \(AOH\) and \(BOH\) are congruent, so \(p = q\), and the line \(OIH\) is a line of symmetry for the diagram.
This means that \(OIH\) is the perpendicular bisector of \(AB\), so \(OIH\) is an altitude of the triangle, and \(C\) lies on \(OHI\). Thus \(ABC\) is isosceles.

