The angle \(A\) of triangle \(ABC\) is a right angle and the sides \(BC\), \(CA\) and \(AB\) are of lengths \(a\), \(b\) and \(c\) respectively. Each side of the triangle is tangent to the circle \(S_1\) which is of radius \(r\). Show that \(2r=b+c-a\).
Let the points where \(S_1\) touches the triangle be \(U\), \(V\) and \(W\) as shown in the diagram. Let the circle have centre \(I\).
The circle \(S_1\) is the incircle of triangle \(ABC\); it’s conventional to label its centre as \(I\).
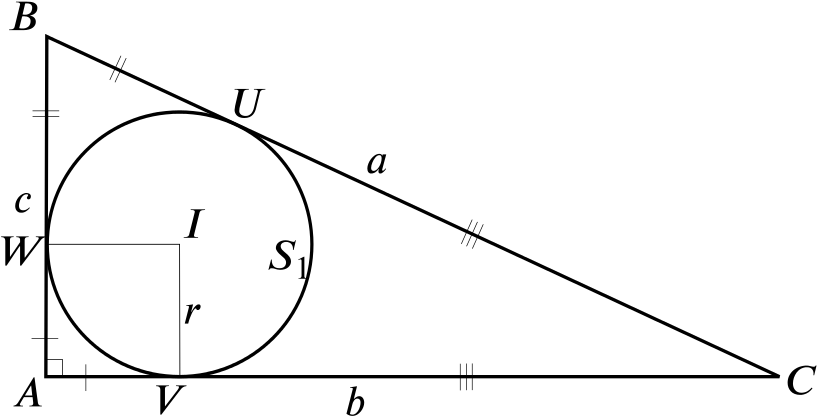
We have lots of tangents to a circle… we know that a tangent to a circle is perpendicular to the circle’s radius at the point of touching.
And we know that if we pick a point not on the circle, and draw the two tangents to the circle from that point, then the distances from the point to the touching points are equal.
Since \[a = CU + BU = b+c-2r,\] we have the required result.
Each vertex of the triangle lies on the circle \(S_2\). The ratio of the area of the region between \(S_1\) and the triangle to the area of \(S_2\) is denoted by \(R\). Show that \[\pi R=-(\pi-1)q^2+2\pi q-(\pi+1),\] where \(q=\dfrac{b+c}{a}\).
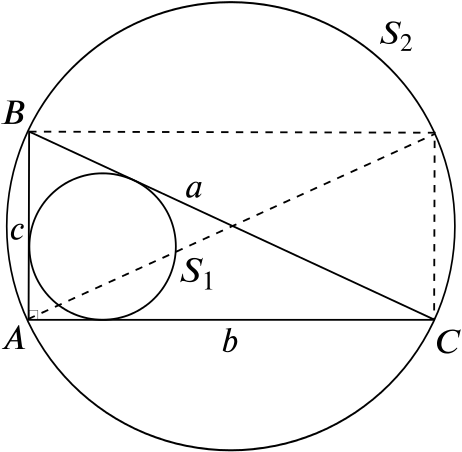
The line segment \(BC\) is the hypotenuse of a right-angled triangle, and so it is the diameter of the circumcircle \(S_2\) of triangle \(ABC\).
Strictly speaking, we are using here the converse of Thales’s theorem (which says that the angle in a semicircle is a right angle).
Thus the radius of the circle \(S_2\) is \(\frac{1}{2}a\). The area of the right-angled triangle \(ABC\) is \(\frac{1}{2}bc\). Circle \(S_1\) has radius \(r\), so has area \(\pi r^2\). Circle \(S_2\) has radius \(\frac{1}{2}a\), so has area \(\frac{1}{4}\pi a^2\).
Remembering the definition of \(R\), this gives \[R=\frac{\frac{1}{2}bc - \pi r^2}{\frac{1}{4}\pi a^2} = \frac{2bc - 4\pi r^2}{\pi a^2}.\]
The question defines \(q = \dfrac{b+c}{a}\), so \(aq=b+c\). This gives \[r=\frac{1}{2}(b+c-a)=\frac{1}{2}a(q-1)\] and so \[\pi R=\frac{2bc - \pi a^2(q-1)^2}{a^2}.\] Now we need to eliminate \(2bc\). Since \(ABC\) is a right-angled triangle, we know \(a^2=b^2+c^2\).
This is Pythagoras’s theorem.
and so \[\frac{2bc}{a^2} = q^2 - 1.\]
Thus \[\begin{align*} \pi R &= \frac{2bc}{a^2} - \pi(q-1)^2\\ &= q^2 - 1 - \pi(q-1)^2\\ &=-(\pi-1)q^2+2\pi q-(\pi+1) \end{align*}\]as required.
Alternatively, we could have substituted \(q=\dfrac{b+c}{a}\) directly into \(-(\pi-1)q^2+2\pi q-(\pi+1)\) and checked that it was equal to \(\pi R\).
Deduce that \[R\leq\frac{1}{\pi(\pi-1)}.\]
The are a number of ways to tackle this.
Approach 1 — Using the discriminant
We know that \(\pi R =-(\pi-1)q^2+2\pi q-(\pi+1)\). We can write this as a quadratic in q: \[(\pi-1)q^2-2\pi q+(\pi+1)+\pi R=0.\] For this to have real values for q, the discriminant must be non-negative. This gives us \[(2\pi)^2 \geq 4(\pi -1)(\pi R +\pi+1)\] which rearranges to give \[R \leq \dfrac{1}{\pi(\pi-1)}\] as required.
Approach 2 — Completing the square
Complete the square on the expression for \(\pi R\): we have \[\begin{align*} \pi R &= -(\pi-1)\left[q^2-\frac{2\pi}{\pi-1}q+\frac{\pi+1}{\pi-1}\right]\\ &= -(\pi-1)\left[\left(q-\frac{\pi}{\pi-1}\right)^2+\frac{\pi+1}{\pi-1}-\frac{\pi^2}{(\pi-1)^2}\right]\\ &= -(\pi-1)\left[\left(q-\frac{\pi}{\pi-1}\right)^2-\frac{1}{(\pi-1)^2}\right] \end{align*}\]and so \[R = \dfrac{1}{\pi(\pi-1)}-(1-\dfrac{1}{\pi})\left(q-\dfrac{\pi}{\pi-1}\right)^2.\]
We can see that \(R\) has a maximum at \(q=\dfrac{\pi}{\pi-1}\), when \(R = \dfrac{1}{\pi(\pi-1)}\) and thus \(R\leq\dfrac{1}{\pi(\pi-1)}\).
Approach 3 — Differentiation
Note — you may not have covered differentiation yet…
To find the stationary value of \(R\) we differentiate the expression for \(\pi R\) with respect to \(q\) and set it equal to zero: we have \[\pi\frac{dR}{dq}=-2q(\pi-1)+2\pi=0\] so \[q=\frac{\pi}{\pi-1}\] We then substitute back into the expression for \(R\) to see that when \(q = \dfrac{\pi}{\pi - 1}\) we have \[\begin{align*} R &= \frac{1}{\pi}\left[-(\pi-1)\frac{\pi^2}{(\pi-1)^2}+\frac{2\pi^2}{\pi-1}-(\pi+1)\right] \\ &= \frac{1}{\pi}\left[\frac{-\pi^2+2\pi^2-(\pi-1)(\pi+1)}{\pi-1}\right] \\ &=\frac{1}{\pi(\pi-1)}. \end{align*}\]We can deduce that this stationary point is a maximum because we have a quadratic in \(q\) where the \(q^2\) term has a negative coefficient.

