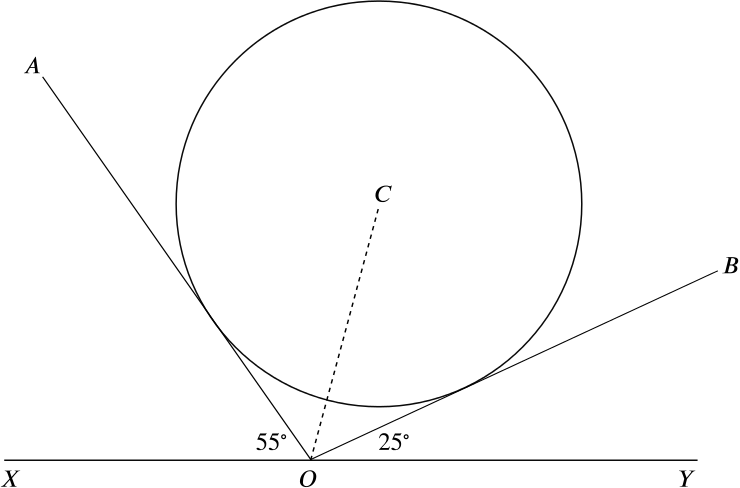
In the diagram, \(OA\) and \(OB\) are tangents to the circle, centre \(C\) and radius \(\quantity{4.5}{in.}\) . The lines \(OA\), \(OB\) are inclined at \(55^\circ\) and \(25^\circ\) respectively to the straight line \(XOY\).
Calculate
- the angle \(COY\);
The angle \(AOB\) is \(100^\circ\), as together with the given angles \(55^\circ\) and \(25^\circ\) it adds up to \(180^\circ\). We now show that the line \(OC\) bisects the angle \(AOB\).
Consider the two triangles \(CDO\) and \(COE\) here:
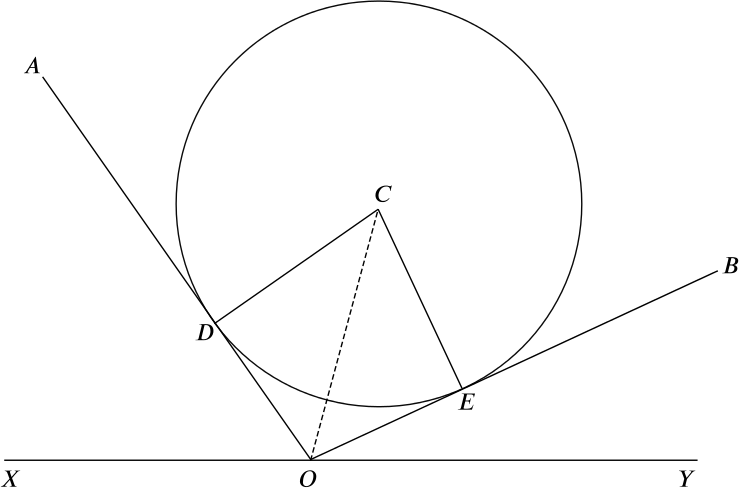
The lines \(CD\) and \(CE\) are radii of the circle. As the tangents to the circle are perpendicular to the radii \(CD\) and \(CE\), the triangles are right-angled at \(D\) and \(E\).
So the two angles are congruent, and corresponding angles and sides have the same size.
In particular, the angles \(DOC\) and \(EOC\) are equal. Therefore the line \(OC\) is an angle bisector and, as the angle \(AOB\) is \(100^\circ\), angle \(EOC\) is \(50^\circ\).
Thus the angle \(COY\) is \(75^\circ\).
- the length \(OC\);
Let’s draw the above triangle \(CDO\).
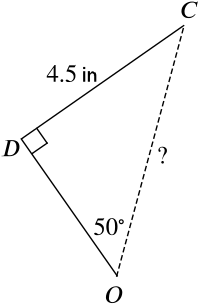
Now by using \(\sin\alpha = \dfrac{\text{opposite}}{\text{hypothenuse}}\), we get \(\sin50^\circ = \dfrac{4.5}{OC}\) and therefore \(OC = \dfrac{4.5}{\sin50^\circ} \approx 5.87\). So the length \(OC\) is approximately \(\quantity{5.87}{in.}\) .
- the distance of \(C\) from the line \(XOY\).
Let’s draw the shortest distance between \(C\) and the line \(XOY\).
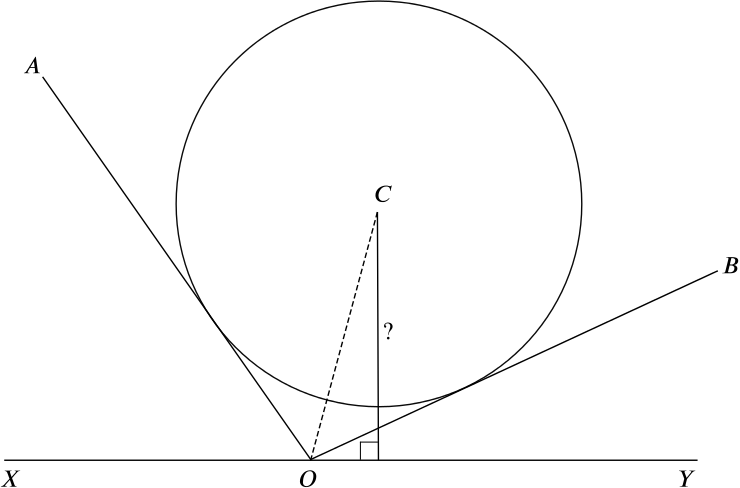
From part (i), we have that the angle \(COY\) is \(75^\circ\), and from part (ii) that \(OC\) is \(\dfrac{4.5}{\sin50^\circ}\) (notice that we are using full accuracy here).
Calling the required distance \(v\), we have
\[\begin{align*} \sin(75^\circ) & = \frac{v}{\left(\dfrac{4.5}{\sin50^\circ}\right)} \\ & = \frac{v\sin50^\circ}{4.5}. \end{align*}\]So \(v = \dfrac{4.5 \sin75^\circ}{\sin50^\circ} \approx \quantity{5.67}{in.}\)

