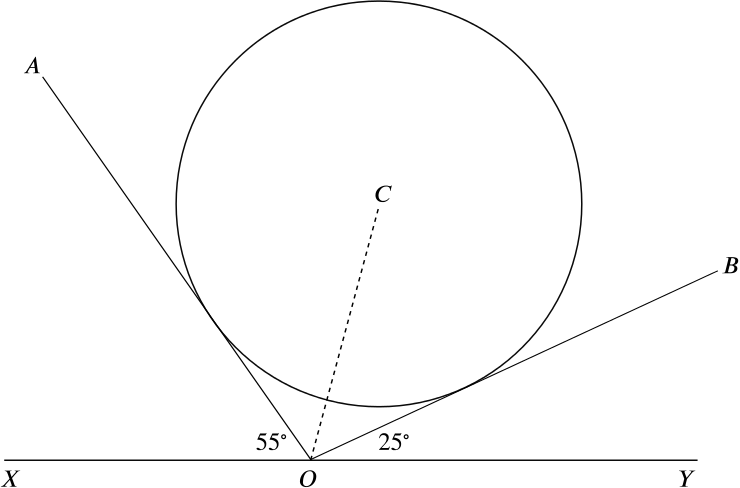
In the diagram, \(OA\) and \(OB\) are tangents to the circle, centre \(C\) and radius \(\quantity{4.5}{in.}\) . The lines \(OA\), \(OB\) are inclined at \(55^\circ\) and \(25^\circ\) respectively to the straight line \(XOY\).
Calculate
- the angle \(COY\);
What does the line \(OC\) do to the angle \(AOB\)? Can you prove this? Which properties of tangents to a circle do you know?
- the distance of \(C\) from the line \(XOY\).
Could we draw in the line we need on our diagram? What can we say now?

