A spider is sitting in the middle of one of the smallest walls in my living room, and a fly is resting by the side of the window on the opposite wall, \(\quantity{2}{m}\) above the floor and \(\quantity{0.5}{m}\) from the adjacent wall.
The room is \(\quantity{8}{m}\) long, \(\quantity{4}{m}\) wide and \(\quantity{3}{m}\) high.
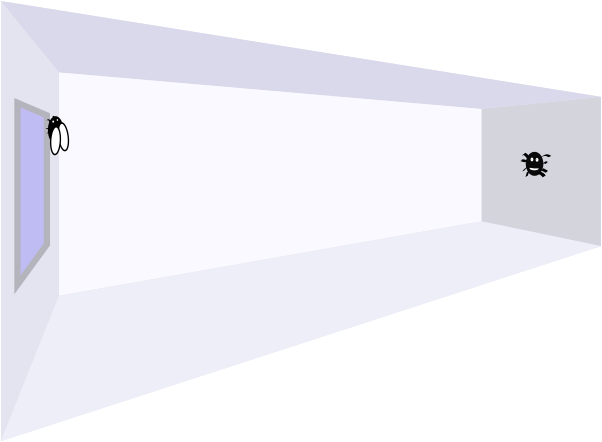
What is the shortest distance the spider could crawl to reach the fly?
(Do check your numerical answer in the Suggestion section before looking at the solution!)
This problem was first posed (with different side lengths) in 1903 by Henry Ernest Dudeney (1857–1931), a brilliant English puzzle creator. His puzzles were popular in his day, and continue to be so. Martin Gardner wrote about his creations, and this puzzle in particular, in Scientific American in 1958; this article was recently republished in Origami, Eleusis, and the Soma Cube: Martin Gardner’s Mathematical Diversions (The New Martin Gardner Mathematical Library). A version of this puzzle also appears on NRICH.
A sequel to this problem appears in The spider and the fly (Part 2).

