A spider is sitting in the middle of one of the smallest walls in my living room, and a fly is resting by the side of the window on the opposite wall, \(\quantity{2}{m}\) above the floor and \(\quantity{0.5}{m}\) from the adjacent wall.
The room is \(\quantity{8}{m}\) long, \(\quantity{4}{m}\) wide and \(\quantity{3}{m}\) high.
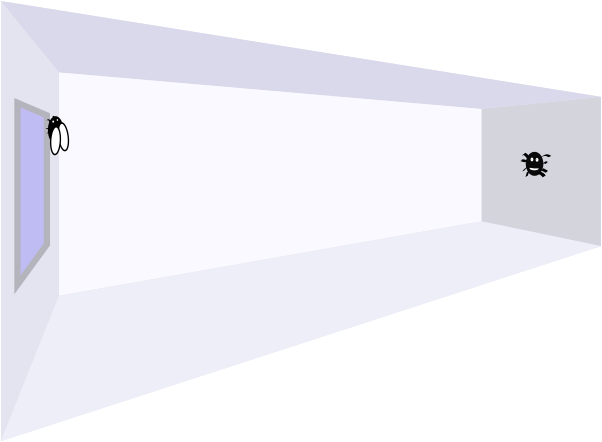
What is the shortest distance the spider could crawl to reach the fly?
In order to solve this problem, let’s consider various possible nets of the room.
Many different nets can be made for the room. Which of them are worth considering for the purposes of this problem?
There are several options. The two obvious ones are that the spider could walk along the wall that the fly is closest to or along the ceiling (since the fly is closer to the ceiling than the floor).
Here are the full nets which correspond to these possibilities:
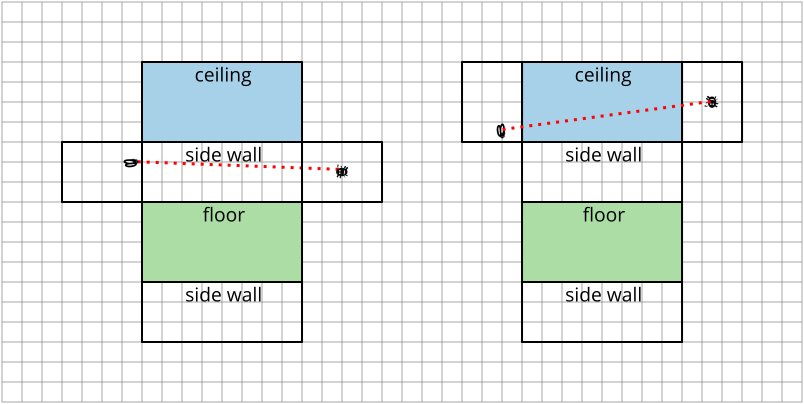
From this sketch, it seems clear that the route via the side wall is the shorter option. We will show the algebraic calculations for both of these to convince ourselves that we are correct.
In the following diagram, we show an enlarged version of the shortest path from the spider to the fly via the side wall. The distances are in metres, and in these more detailed nets, we have only shown the walls, ceiling and floor if the spider walks across them.
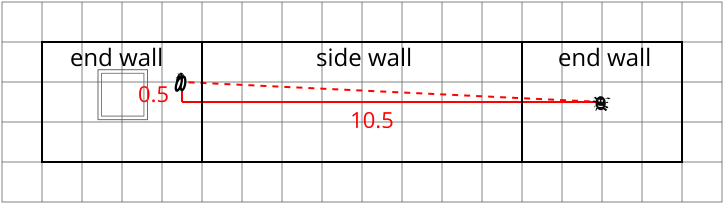
We can use Pythagoras’ theorem to find the distance that the spider must walk using this route: \[\text{distance the spider walks}= \sqrt{10.5^2+0.5^2}= \sqrt{\vphantom{()}110.5}\approx \quantity{10.51}{m}.\]
In the next diagram, we consider the shortest path from the spider to the fly along the ceiling.
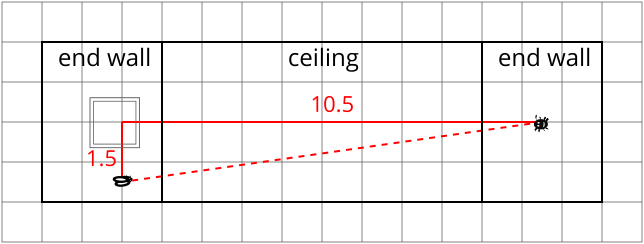
It is clear by comparing the last two drawings that this path is longer; were we to use Pythagoras to find the distance, we would obtain: \[\text{distance the spider walks} = \sqrt{10.5^2+1.5^2}=\sqrt{\vphantom{()}112.5}\approx \quantity{10.61}{m}.\]
This shows us numerically that the route along the wall is shorter than the route along the ceiling.
There are other possible nets for this, though, obtained by combining the two earlier nets. In the following drawing, we have superimposed the two nets, with the end walls drawn solidly when attached to the ceiling and dashed when attached to the side wall:
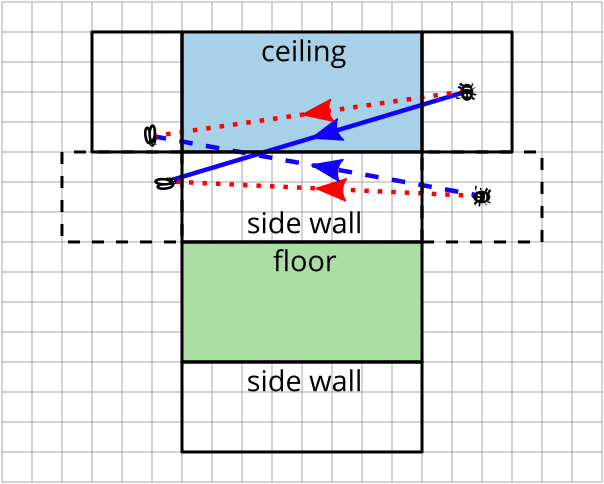
We have drawn our original two spider routes as red dotted lines, and the two new possible routes in blue (one solid, one dashed).
It is clear that the dashed blue line route is longer than the direct (red dotted) route via the side wall, as both the “horizontal” and “vertical” distances travelled are greater in the former route. However, it is not so clear whether or not the solid blue line route is longer or shorter than the direct side wall route: the “horizontal” distance is shorter, but the “vertical” distance is greater.
So let’s see if this new route is shorter. Here again is a more detailed net showing just the part of the room the spider walks across.
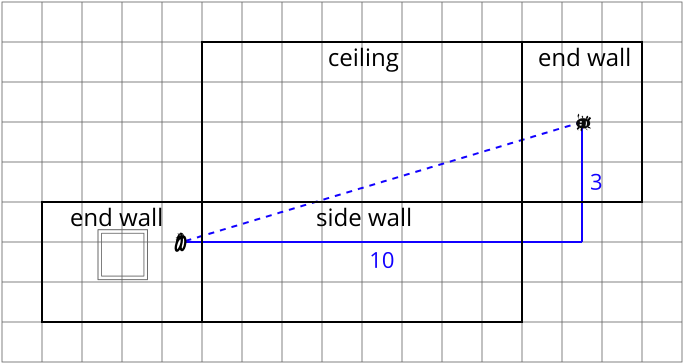
Using Pythagoras, we find \[\text{distance the spider walks}=\sqrt{10^2+3^2}= \sqrt{109}\approx \quantity{10.44}{m}.\] So this route is even shorter than the other two, and we have found the shortest possible route.
It is interesting to note that we were comparing the two sums \[10.5^2+0.5^2\ \text{and}\ 10^2+3^2.\] Although \(10.5\) is only slightly larger than \(10\), the effect of squaring makes this more significant than the increase of \(0.5\) to \(3\).
You might like to check other possible nets and their routes to convince yourself that we cannot do any better than this.

