For each set of points determine what sort of triangle the three coordinates form (equilateral, isosceles, right-angled and scalene). How many of each type are there in the sets of coordinates given below?
We can use Pythagoras to find the distances between pairs of points, and therefore all we need to solve the question. But do we need to? If we don’t rush into crunching the numbers, then we might find some logic, reasoning and other areas of maths can help us arrive at an answer. Can we still find all the answers without using Pythagoras to calculate a distance?
- \((9,-2)\), \((4,6)\), \((20,16)\).

By sketching the triangle we should see that this seems not to be equilateral. Although do remember your sketches are not accurate, so don’t dismiss anything too quickly!
If we label the horizontal and vertical distances between points we can learn a lot more.
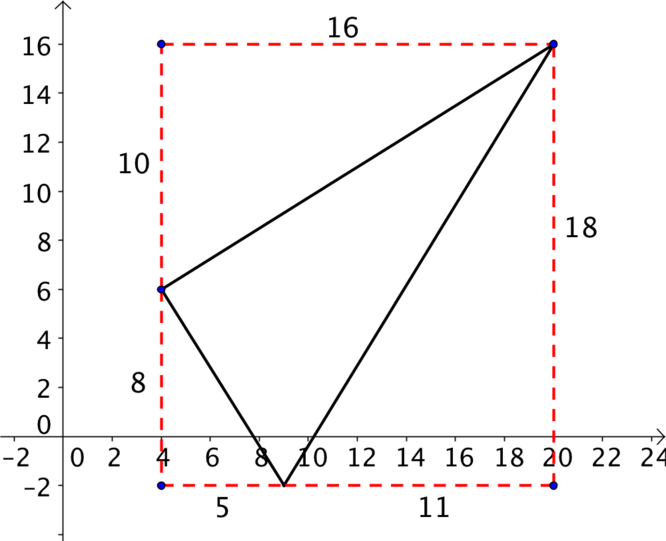
If we look at the triangles formed above, we might notice that two of the triangles are similar.
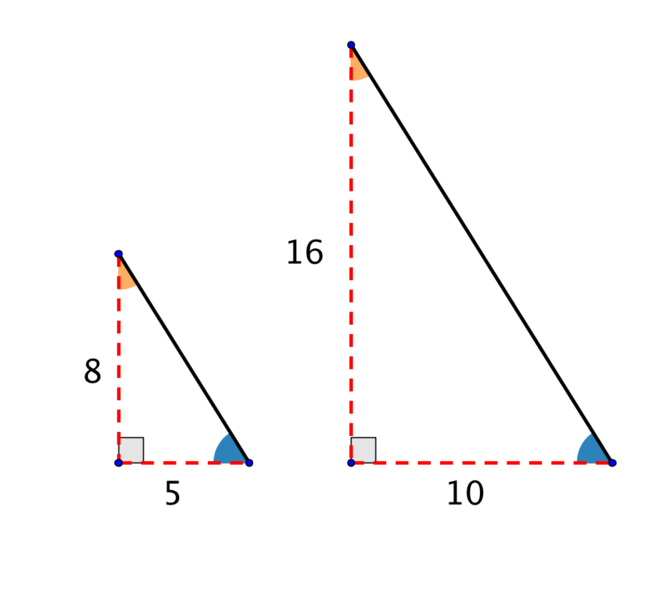
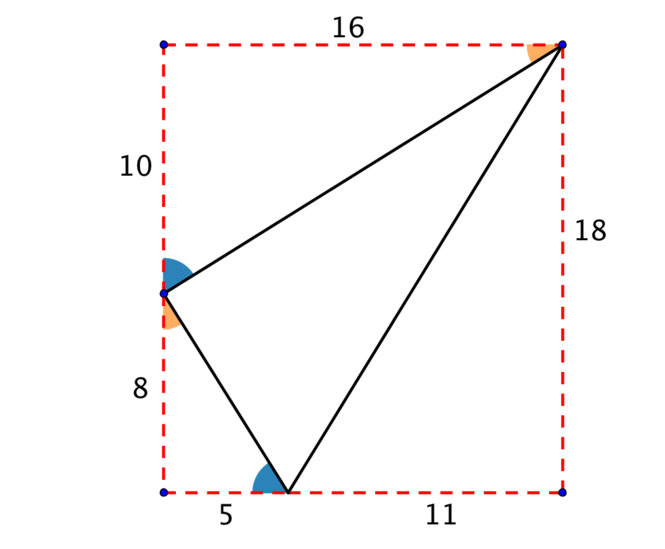
- Can you use the diagrams above to prove the original triangle must be right-angled?
Thinking about the three right-angled triangles formed by the dotted lines, we can see that they all have different length hypotenuses.
You can have two different right-angled triangles with the same length hypotenuse, e.g. 7,24,25 and 15, 20, 25, but in these three cases, both sides are smaller (or larger) than the comparable side in the other triangles, for example, \(10<11\) and \(16<18\) so \(\sqrt{10^2+16^2}<\sqrt{11^2+18^2}\).
- Do these different approaches tell you all you need to know by themselves? Or do you have to use a combination of both to find out what type of triangle it is?
- \((3, 0)\), \((-1, 0)\), \((1,21)\).
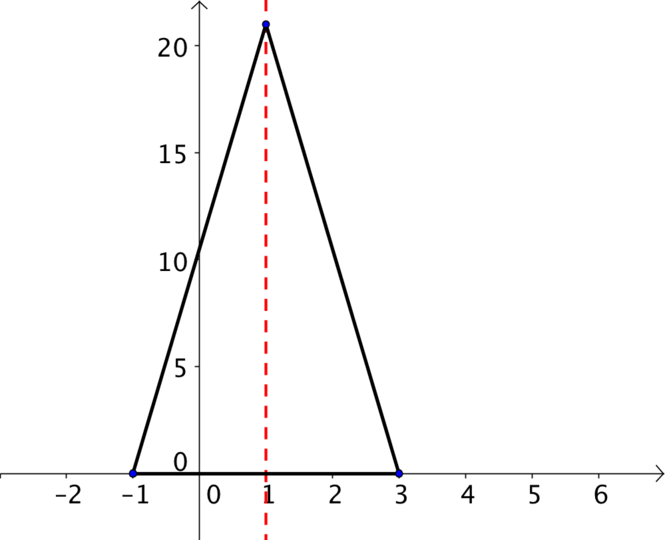
Our sketch here is very revealing. Clearly the triangle has a line of symmetry about \(x = 1\) and is therefore isosceles. As the base length is \(4\) units, it must be shorter than the other two sides and so is not equilateral.
Finally we need to check if it has a right-angle. If your triangle has a right-angle, then the side opposite it is the longest. Can you see why this triangle cannot be right-angled?
- \((1,1)\), \((3,2)\), \((2,4)\).
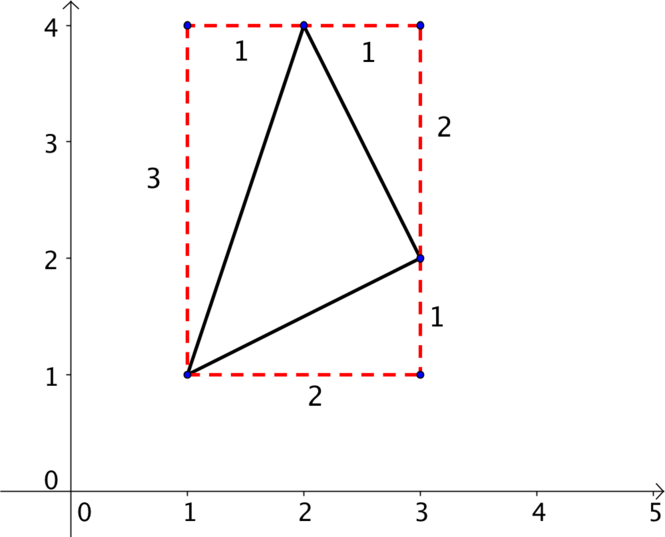
An initial sketch of these points does not reveal much, but adding in the additional triangles enables us to see that it is an isoscles triangle, as two of these triangles are congruent.
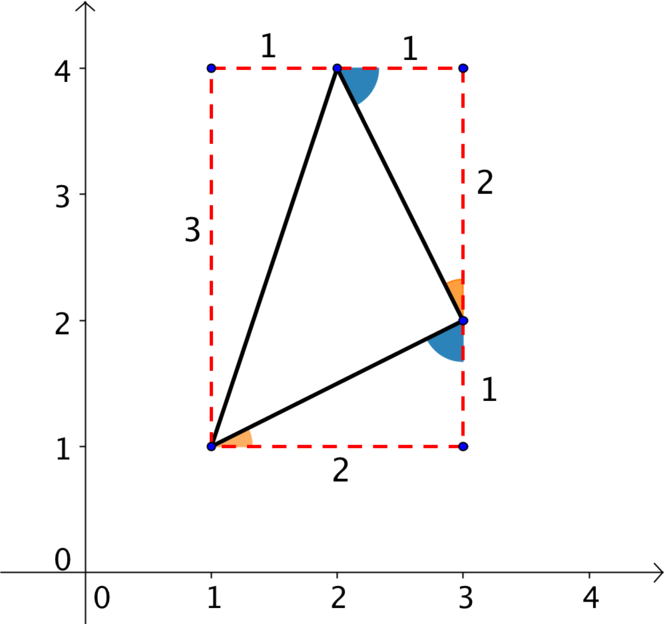
Can you use the congruent triangles in the image above to prove that this is a right-angled triangle?
Or perhaps you might want to calculate the gradients. What do you know about perpendicular lines?
- \((0, 3)\), \((0, 15)\), \((6\sqrt{3}, 9)\).
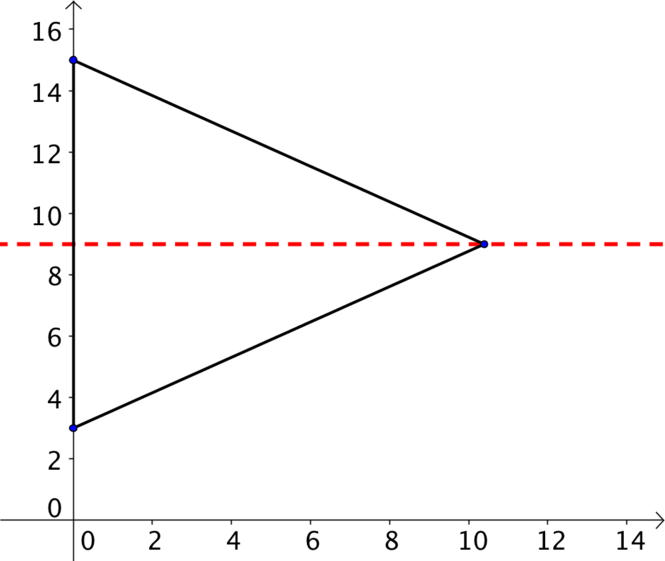
As we sketch we should notice that \(y=9\) is a line of symmetry and therefore the triangle will be isosceles. It doesn’t appear to be right-angled, but it looks like it could be equilateral so we will check that first.
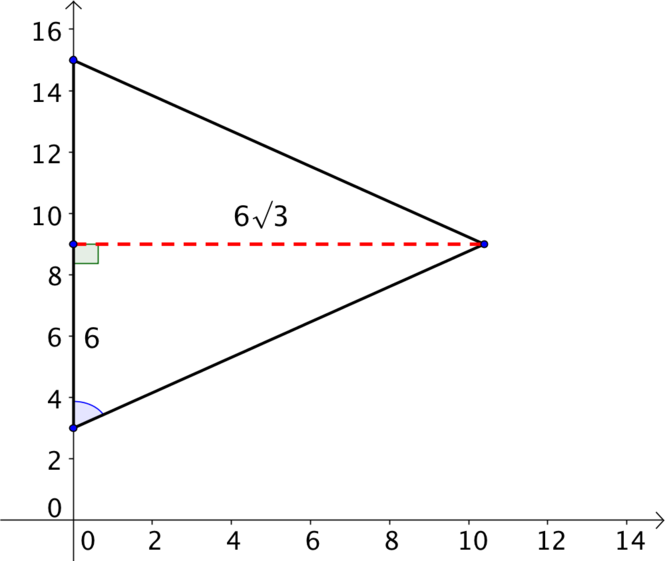
If it is equilateral then the marked angle must be \(60^{\circ}\). What can we use to calculate the angle and see if the triangle is equilateral?
- \((-2,-7)\), \((1, -1)\), \((5,7)\).

It is likely that you drew a sketch that looked a little like this. You might have spotted that all the coordinate pairs have the relationship \(y = 2x-3\) and therefore the points must all lie in a straight line.
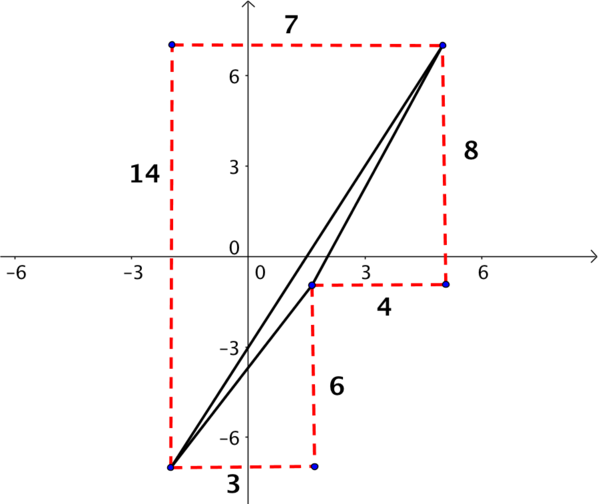
You might have drawn these triangles, and spotted that all of them are similar, and therefore the hypotenuses have the same gradient. Or you might have just worked out the gradients of two of the triangles and found that they were the same, and therefore parallel.
If two line segments are parallel then they cannot form part of a triangle. If two line segments are parallel and share a common point, then they must lie on the same line. Either way, no triangle is formed by these three points.
- \((2, -3)\), \((-1, 1)\), \((-4, 8)\).

It looks fairly clear that this is not an equilateral or right-angled triangle, but can you explain why this must be the case? Think about the gradients of the lines.
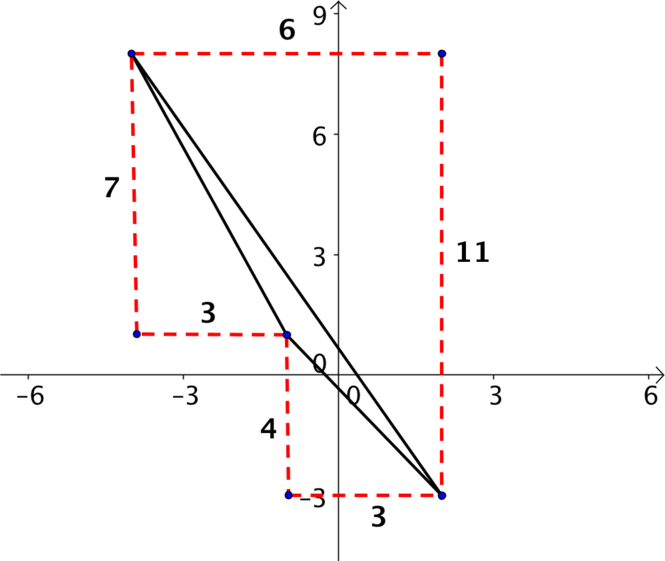
The only remaining question is whether it is isosceles. Looking at the right-angled triangles that can give us the lengths, we can see that \(\sqrt{3^2+4^2}<\sqrt{3^2+7^2}<\sqrt{6^2+11^2}\) which means none of the lengths are the same, so it is a scalene triangle.
Think about the different approaches we have taken in the solutions. They get us to the same answer, but the journeys are very different.
- Which approach did you start with?
- After seeing different methods, which do you prefer? Why?
- What strategies and ideas from the approaches could you take forward and apply to new problems?

