For each set of points determine what sort of triangle the three coordinates form (equilateral, isosceles, right-angled and scalene). How many of each type are there in the sets of coordinates given below?
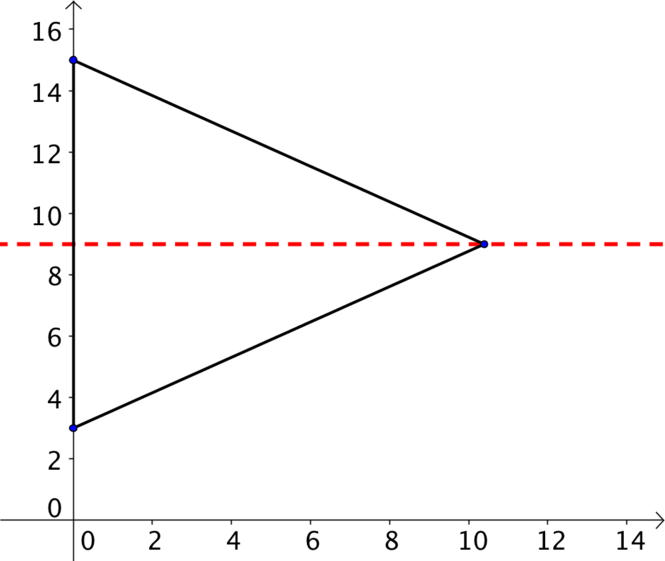
We can use Pythagoras to find the distance between the points, to see if any side lengths are the same. We might also sketch the points to get a sense of what the triangle might look like. For example in part (d) a quick sketch should reveal that \(y=9\) is a line of symmetry and therefore the triangle is isosceles.
- \((9,-2)\), \((4,6)\), \((20,16)\).
The distances between the points are \[\sqrt{5^2 + 8^2} = \sqrt{25 + 64} = \sqrt{89}\] and \[\sqrt{11^2 + 18^2} = \sqrt{121 + 324} = \sqrt{445}\] and \[\sqrt{16^2 + 10^2} = \sqrt{256 + 100} = \sqrt{356},\] so we see that the triangle is scalene (all the sides have different lengths).
Now we know it is scalene - but is that all it is? A triangle with three different side lengths can also have a right-angle.
We can use the converse of Pythagoras’s theorem (use the result ‘backwards’) to check whether the triangle is right-angled: the triangle is right-angled if and only if its side lengths satisfy the Pythagorean equation.
The longest side has length \(\sqrt{445}\), so if the triangle is right-angled then that must be the hypotenuse. We have \[(\sqrt{89})^2 + (\sqrt{356})^2 = 89 + 356 = 445 = (\sqrt{445})^2,\] so the triangle is right-angled and scalene.
- \((3, 0)\), \((-1, 0)\), \((1,21)\).
The distances between the points are \[4\] and \[\sqrt{2^2 + 21^2} = \sqrt{4 + 441} = \sqrt{445}\] and \[\sqrt{2^2 + 21^2} = \sqrt{445},\] so the triangle is isosceles but not equilateral.
It is possible for a triangle to be isosceles and right-angled. However it is not necessary to use the converse of Pythagoras’s theorem here - can you see why this won’t be right-angled without doing any calculations?
- \((1,1)\), \((3,2)\), \((2,4)\).
The distances between the points are \[\sqrt{2^2 + 1^2} = \sqrt{4 + 1} = \sqrt{5}\] and \[\sqrt{1^2 + 3^2} = \sqrt{1 + 9} = \sqrt{10}\] and \[\sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5},\] so we see that the triangle is isosceles but not equilateral.
Unlike the example above, the equal length sides are not the longest. Therefore this could be a right-angled triangle and we need to check using Pythagoras.
If the triangle is right-angled, then the right angle must be between the two sides with the same length, so we would need \[(\sqrt{5})^2 + (\sqrt{5})^2 = (\sqrt{10})^2.\]
\[(\sqrt{5})^2 + (\sqrt{5})^2 = 5 + 5 = 10 = (\sqrt{10})^2,\]
so this does indeed hold, and the triangle is both isosceles and right-angled.
- \((0, 3)\), \((0, 15)\), \((6\sqrt{3}, 9)\).
This is the question we sketched at the start and determined it was isosceles.
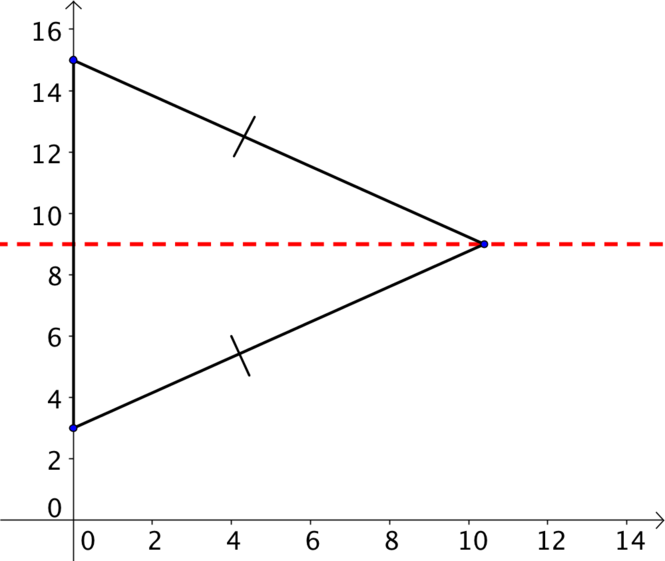
This means we only need to check two sides to determine if it is equilateral.
The distances between the points on the left hand side is \[12\] and choosing one of the other two sides the distance is \[\sqrt{(6\sqrt{3})^2 + 6^2} = \sqrt{108 + 36} = \sqrt{144} = 12\] so we see that the triangle is equilateral (and hence also isosceles).
Since the triangle is equilateral, its angles are all \(60^{\circ}\), and so it cannot have a right angle.
The definition of an isosceles triangle is that it has at least two equal sides and two equal angles. Therefore an equilateral triangle is a special case of an isosceles triangle - just like a square is a special case of a rectangle.
- \((-2,-7)\), \((1, -1)\), \((5,7)\).
Did you do any calculations for this? You might have sketched the points and noticed it didn’t look like a triangle. If you spotted all the coordinate pairs had the relationship \(y = 2x - 3\) then you didn’t need to calculate the distances.
If you calculate the distances you find they are \[\sqrt{3^2 + 6^2} = \sqrt{9 + 36} = \sqrt{45}= 3\sqrt{5}\] and \[\sqrt{4^2 + 8^2} = \sqrt{16 + 64} = \sqrt{80} = 4\sqrt{5}\] and \[\sqrt{7^2 + 14^2} = \sqrt{49 + 196} = \sqrt{245} = 7\sqrt{5}\]
If we add the first two distances together, we get the third. \[3\sqrt{5}+4\sqrt{5}=7\sqrt{5}\]
Whatever method you used, the conclusion is that drawing a triangle would be impossible, as these three points lie in a straight line.
- \((2, -3)\), \((-1, 1)\), \((-4, 8)\).
The distances between the points are \[\sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\] and \[\sqrt{6^2 + 11^2} = \sqrt{36 + 121} = \sqrt{157}\] and \[\sqrt{3^2 + 7^2} = \sqrt{9 + 49} = \sqrt{58},\] so we see that the triangle is scalene.
The longest side has length \(\sqrt{157}\), so if the triangle is right-angled then that must be the hypotenuse. But \[5^2 + (\sqrt{58})^2 = 25 + 58 = 83 \neq (\sqrt{157})^2,\] so the triangle is not right-angled.
In summary:
| Points | Equilateral | Isosceles | Scalene | Right-angled |
|---|---|---|---|---|
|
Y | Y | ||
|
Y | |||
|
Y | Y | ||
|
Y | Y | ||
|
||||
|
Y | |||
| Total | 1 | 3 | 2 | 2 |
These solutions use a lot of calculations, and a little bit of reasoning. Perhaps there is a different way? Take a look at the alternative solutions section to find out.

