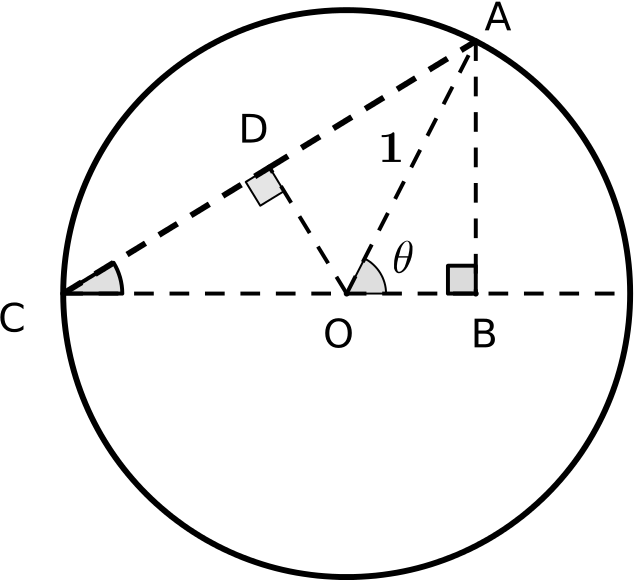
Take a look at the identities below.
\[ \cos^2 \frac{\theta}{2} \equiv \frac{1}{2}(1+\cos \theta) \quad \quad \quad \sin^2 \frac{\theta}{2} \equiv \frac{1}{2}(1-\cos \theta)\]
You may well know enough trigonometric identities to be able to prove these results algebraically, but you could also prove them using geometry. We have provided some diagrams that may help you to prove the result for \(\cos^2 \frac{\theta}{2}\). Can you link the diagrams together to form a proof?
You may find it helpful to group the diagrams together in different ways or look for links between pairs of diagrams. You don’t need to use all the diagrams in your proof and you may prefer to add some of your own diagrams. The diagrams are available as a print out. There is an extra card in case you’d like to include another diagram in your proof.
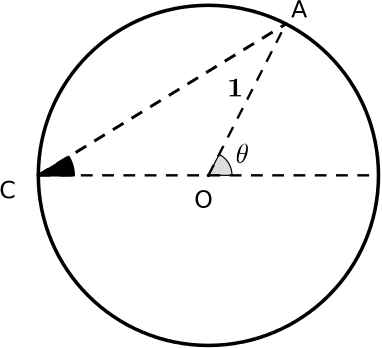
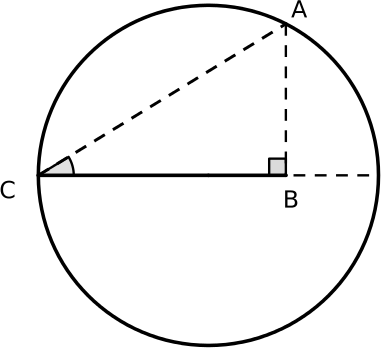
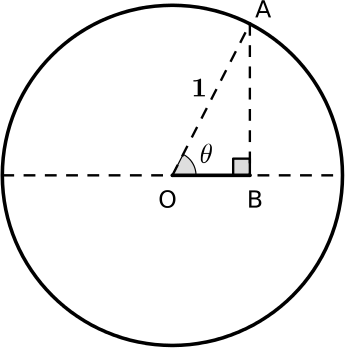
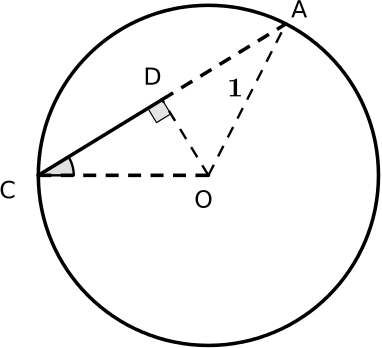
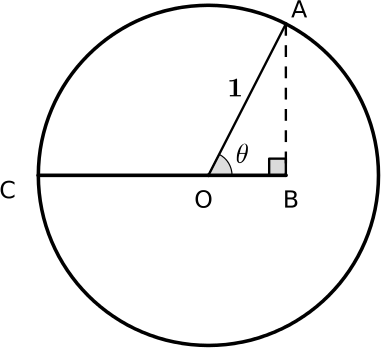
Can you prove the result for \(\sin^2 \frac{\theta}{2}\) in a similar way?