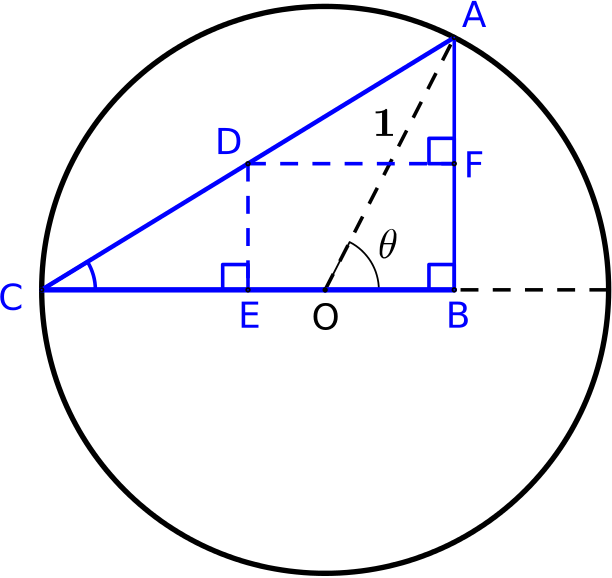
Take another look at the identities.
\[ \cos^2 \frac{\theta}{2} \equiv \frac{1}{2}(1+\cos \theta) \quad \quad \quad \sin^2 \frac{\theta}{2} \equiv \frac{1}{2}(1-\cos \theta)\]
The first says that \(\cos^2 \frac{\theta}{2}\) is the mean of \(1\) and \(\cos \theta\). What does this tell you geometrically?
Can you use the same ideas to think about the identity for \(\sin^2 \frac{\theta}{2}\)?
Can you draw a diagram to illustrate the following results for \(\tan \frac{\theta}{2}\)? \[\tan \frac{\theta}{2} \equiv \frac{\sin \theta}{1+\cos \theta}\] and \[\tan \frac{\theta}{2}\equiv \frac{1-\cos \theta}{\sin \theta}\]
For which values of \(\theta\) are these identities true?