Prove that, if \(t=\tan\tfrac{1}{2}\theta\), then \[\sin\theta=\frac{2t}{1+t^2}...\]
Approach 1: Starting with the left hand side
We can rewrite \(\sin\theta\) by using the double angle formula: \[\sin\theta= \sin\bigl(2(\tfrac{1}{2}\theta)\bigr)= 2\sin\tfrac{1}{2}\theta \cos\tfrac{1}{2}\theta.\]
In order to get \(t\) (which we want in the numerator) into the identity, we can rewrite \[\sin\tfrac{1}{2}\theta=\tan\tfrac{1}{2}\theta \cos\tfrac{1}{2}\theta,\] which is \(t\cos\tfrac{1}{2}\theta\) (where we have used \(t=\tan\tfrac{1}{2}\theta\)). Therefore, \[\sin\theta=2t\cos^2\tfrac{1}{2}\theta.\]
Since we want \(t\) in the denominator as well, we write \[\cos^2\tfrac{1}{2}\theta=\frac{1}{\sec^2\tfrac{1}{2}\theta}.\] Using the identity \[1+\tan^2\tfrac{1}{2}\theta=\sec^2\tfrac{1}{2}\theta,\] we deduce that \[\cos^2\tfrac{1}{2}\theta=\frac{1}{1+\tan^2\tfrac{1}{2}\theta} =\frac{1}{1+t^2}.\] Therefore \[\sin\theta=\frac{2t}{1+t^2}.\]
Approach 2: Starting with the right hand side
We will rewrite the right hand side in terms of \(\sin\dfrac{1}{2}\theta\) and \(\cos\dfrac{1}{2}\theta\). We have \[\begin{align*} \frac{2t}{1+t^2}&= \frac{2\dfrac{\sin\frac{1}{2}\theta}{\cos\tfrac{1}{2}\theta}} {1+\dfrac{\sin^2\frac{1}{2}\theta}{\cos^2\frac{1}{2}\theta}}\\ &=\frac{2\sin\tfrac{1}{2}\theta \cos\tfrac{1}{2}\theta} {\cos^2\tfrac{1}{2}\theta+\sin^2\tfrac{1}{2}\theta}, \end{align*}\]where we reached the second line by multiplying the numerator and denominator of the large fraction by \(\cos^2\dfrac{1}{2}\theta\).
Since \(\sin^2\tfrac{1}{2}\theta+\cos^2\tfrac{1}{2}\theta=1\), the denominator is \(1\) and hence \[\frac{2t}{1+t^2}=2\sin\tfrac{1}{2}\theta \cos\tfrac{1}{2}\theta=\sin\theta,\] as required.
\[\text{...and}\quad\cos\theta=\frac{1-t^2}{1+t^2}.\]
As in Approach 1, we write \(\tan\theta=\tan\left(2\left(\dfrac{1}{2}\theta\right)\right)\), and use the double-angle formula for \(\tan\) to get \[\tan\theta=\frac{2\tan\tfrac{1}{2}\theta}{1-\tan^2\tfrac{1}{2}\theta}=\frac{2t}{1-t^2}.\]
We also know that \(\tan\theta=\dfrac{\sin\theta}{\cos\theta}\), so that \(\cos\theta=\dfrac{\sin\theta}{\tan\theta}\).
Therefore, using our expressions for \(\sin\theta\) and \(\tan\theta\) in terms of \(t\), we deduce \[\cos\theta=\frac{\left(\dfrac{2t}{1+t^2}\right)}{\left(\dfrac{2t}{1-t^2}\right)}=\frac{1-t^2}{1+t^2}.\]
We can also prove that \(\cos\theta=\dfrac{1-t^2}{1+t^2}\) using Approaches 1 and 2 above.
By expressing \(\dfrac{3+\cos\theta}{\sin\theta}\) in terms of \(t\), or otherwise, show that this expression cannot have any value between \(-2\sqrt{2}\) and \(+2\sqrt{2}\).
Method 1
We have \[\begin{align*} \frac{3+\cos\theta}{\sin\theta} &=\frac{3+\dfrac{1-t^2}{1+t^2}}{\dfrac{2t}{1+t^2}}\\ &=\frac{3(1+t^2)+1-t^2}{2t}\\ &=\frac{4+2t^2}{2t}\\ &=\frac{2+t^2}{t}. \end{align*}\]We need to show therefore that \(\dfrac{2+t^2}{t}=t+\dfrac{2}{t}\) cannot have any value in the given range, where \(t\) is any real number except for zero.
The last part is because \(t=\tan\tfrac{1}{2}\theta\) can take any real value, but we cannot allow \(t=0\) in this fraction, just as we cannot allow \(\sin\theta=0\) in the original fraction. We have
\[\sin\theta \neq 0 \implies \tan\frac{1}{2}\theta \neq 0.\]
Let \(t+\dfrac{2}{t} = k\). Then \(t^2-kt+2=0\), and for this to have real roots, the discriminant must be non-negative.
This means that \(k^2 \geq 8\), and so \(k \geq 2\sqrt{2}\), or \(k \leq -2\sqrt{2}\), as required.
Method 2
If we sketch a graph of \(y=t+\dfrac{2}{t}\), we see that it has an asymptote at \(t=0\), is positive for \(t>0\) and negative for \(t<0\).
For \(t>0\), it tends to \(\infty\) as \(t\to\infty\) and as \(t\to 0\); for \(t<0\), it tends to \(-\infty\) as \(t\to-\infty\) and as \(t\to0\). So the graph looks something like this:
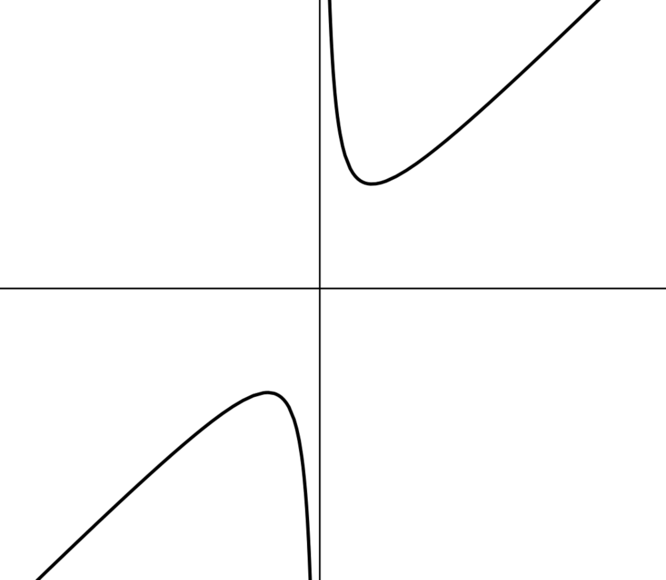
We can find the stationary points using calculus.
Writing \(y=t+\dfrac{2}{t}\), we have \(\dfrac{dy}{dt}=1-\dfrac{2}{t^2}\), so\(\dfrac{dy}{dt}=0\) has solutions \(t=\pm\sqrt{2}\).
When \(t=\sqrt{2}\), \(y=\sqrt{2}+\dfrac{2}{\sqrt{2}}=2\sqrt{2}\); when\(t=-\sqrt{2}\), \(y=-2\sqrt{2}\).
So referring back to our sketch graph, we see that \(y\) cannot take anyvalues between \(-2\sqrt{2}\) and \(+2\sqrt{2}\).
Method 3
Another calculus-free approach is to use the arithmetic mean–geometric mean (AM–GM) inequality.
This says that if \(a_1\) and \(a_2\) are positive real numbers, then their arithmetic mean is greater than or equal to their geometric mean.
In other words, \(\dfrac{a_1 + a_2}{2} \geq \sqrt{a_1a_2}\) where \(a_1, a_2 \geq 0\), with equality if and only if \(a_1 = a_2\).
In our case, if we take \(n=2\) and set \(a_1=t\) and \(a_2=\frac{2}{t}\), we find that \[\frac{t+\frac{2}{t}}{2}\ge \sqrt{t \times\frac{2}{t}}=\sqrt{2},\] with equality if and only if \(t=\dfrac{2}{t}\).
Thus for positive values of \(t\), \(t+\dfrac{2}{t}\ge 2\sqrt{2}\) with equality if and only if \(t=\dfrac{2}{t}\), that is, if \(t=\sqrt{2}\).
For negative values of \(t\), let \(t=-u\), with \(u\) positive. Then \(t+\dfrac{2}{t}=-u-\dfrac{2}{u}=-\left(u+\dfrac{2}{u}\right)\).
Since \(u+\dfrac{2}{u}\ge2\sqrt{2}\), it follows that for negative values of \(t\), \(t+\dfrac{2}{t}\le -2\sqrt{2}\) with equality if and only if \(t=-\sqrt{2}\).
Thus \(t+\dfrac{2}{t}\) cannot take any values between \(-2\sqrt{2}\) and\(+2\sqrt{2}\).
Method 4
As a final method, if \(t\) is positive, we can write \(t+\dfrac{2}{t}\) as \[t+\frac{2}{t}=\left(\sqrt{t}-\sqrt{\frac{2}{t}}\right)^2+2\sqrt{2}.\] Since a square is always positive or zero, the right hand side must be at least \(2\sqrt{2}\), with equality if and only if\(\sqrt{t}=\sqrt{\dfrac{2}{t}}\).
We can deal with the case of \(t\) negative as above.
What could make us think to write \(t+\dfrac{2}{t}\) in such a bizarre way? And what made us think that it would be useful?
To prove the AM–GM inequality for \(n=2\), we first observe that \[(x-y)^2=x^2+y^2-2xy,\] so that \[x^2+y^2=(x-y)^2+2xy\ge 2xy\] with equality if and only if \(x=y\).
If we now write \(x=\sqrt{\vphantom{0}a_1}\) and\(y=\sqrt{\vphantom{0}a_2}\), we get \[a_1+a_2\ge 2\sqrt{\vphantom{0}a_1a_2},\] which is, on dividing by \(2\), the AM–GM inequality for \(n=2\).
So in this approach, we have simply replicated this proof without mentioning the AM–GM inequality!

