A tower stands on a river bank. From a point on the other bank directly opposite, and at height \(h\) above the water level, the angle of elevation of the top of the tower is \(\alpha\) and the angle of depression of the reflection of the top in the water is \(\beta\). [It is to be assumed that the water is smooth, so that the reflection of any object in the water will appear to be as far below the surface as the tower is above it.] Prove that the height of the top of the tower above the water is \[h\sin(\alpha+\beta)\cosec(\beta-\alpha),\] and that the width of the river is \[2h\cos\alpha\cos\beta\cosec(\beta-\alpha).\]
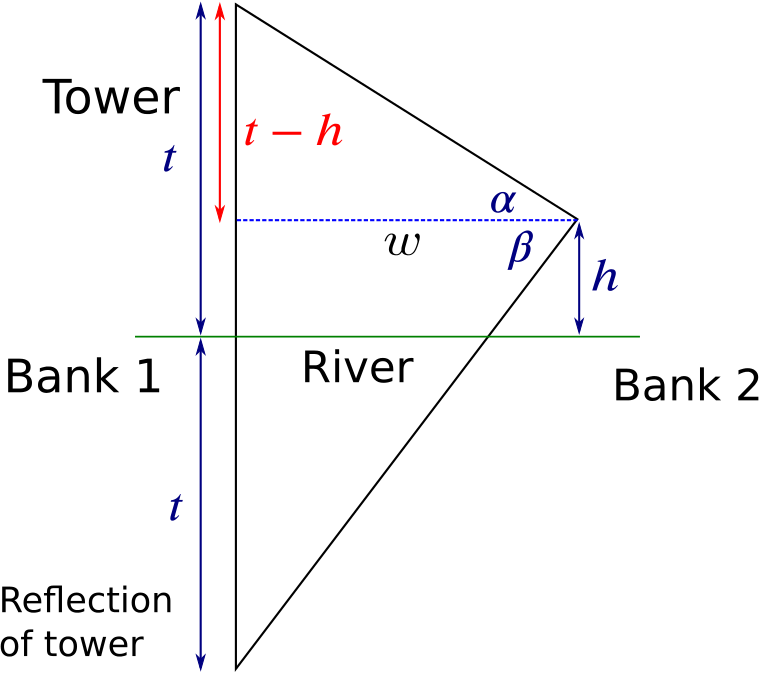
The question wants us to find the height of the tower, \(t\), and the width of the river, \(w\). It’s as if someone of height \(h\) is measuring \(\alpha\) and \(\beta\) using a theodolite, and is then using these three values to calculate \(t\) and \(w\). Notice how we deal with the reflection of the tower in our diagram.
We have two right-angled triangles we can work with from the picture. We have
\[\begin{equation} \tan\alpha=\frac{t-h}{w} \label{eq:1}, \end{equation}\] from the top triangle, and \[\begin{equation} \tan\beta=\frac{t+h}{w} \label{eq:2}, \end{equation}\]from the bottom triangle.
We will first find the height of the tower, \(t\). Rearranging \(\eqref{eq:2}\) we find that \[w=\frac{t+h}{\tan\beta}.\]
Substituting this value of \(w\) into equation \(\eqref{eq:1}\) yields \[\begin{align*} \tan\alpha&=\frac{(t-h)\tan\beta}{t+h} \\ \implies (t+h)\tan\alpha&=(t-h)\tan\beta \\ \implies (t+h)\sin\alpha\cos\beta&=(t-h)\sin\beta\cos\alpha \\ \implies t&=\frac{-h(\sin\alpha\cos\beta+\sin\beta\cos\alpha)}{\sin\alpha\cos\beta-\sin\beta\cos\alpha}, \\ \implies t&=\frac{h\sin(\alpha+\beta)}{\sin(\beta-\alpha)}=h\sin(\alpha+\beta)\cosec(\beta-\alpha). \end{align*}\]Now we wish to find the width of the river, \(w\). We now know what \(t\) is, so we have, using our expression for \(w\) above, \[w=\frac{t+h}{\tan\beta}=\frac{h\sin(\alpha+\beta)\cosec(\beta-\alpha)+h}{\tan\beta}.\]
So we must now rearrange this to check that this agrees with the answer in the question. We have \[\begin{align*} w&=h\left(\frac{\sin(\alpha+\beta)\cos\beta}{\sin{\beta\sin(\beta-\alpha)}}+\frac{\cos\beta}{\sin\beta}\right), \\ &=h\cos\beta\left(\frac{\sin(\alpha+\beta)+\sin(\beta-\alpha)}{\sin\beta\sin(\beta-\alpha)}\right), \\ &=h\cos\beta\left(\frac{2\sin\beta\cos\alpha}{\sin\beta\sin(\beta-\alpha)}\right), \\ &=2h\cos\alpha\cos\beta\cosec(\beta-\alpha), \end{align*}\]as required.
Alternatively we can use the identity \[\sin\theta+\sin\phi=2\sin\left(\frac{\theta+\phi}{2}\right)\cos\left(\frac{\theta-\phi}{2}\right).\]
Find these two distances (to the nearest foot) when \(h=\quantity{15}{ft.}\), \(\alpha=24^\circ\), and \(\beta=31^\circ\).
to the nearest foot (using a calculator).
We need to make sure our calculator is in the correct mode (degrees or radians) before making the computation.

