- Prove that \[\cos(A+B)=\cos A\cos B - \sin A\sin B,\] where the angles \(A\), \(B\) and \(A+B\) are all acute.
We’ll use \(\alpha\) and \(\beta\) to represent the angles, and capital letters to represent points on the diagram. So we are trying to prove that
\[\cos(\alpha+\beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta.\]
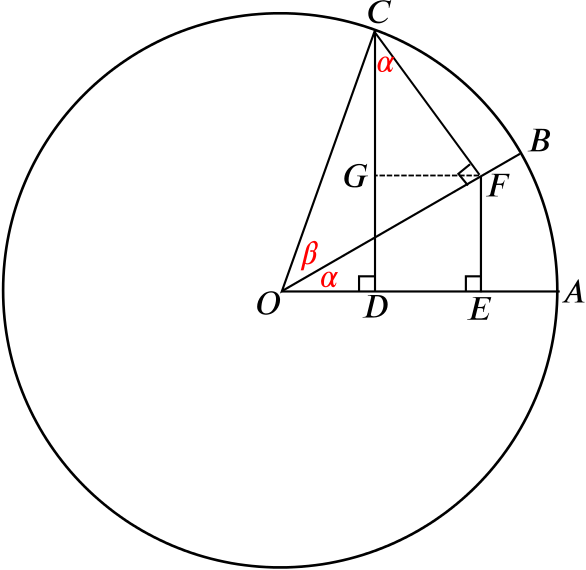
The circle drawn has radius \(1\) (it’s a unit circle). From triangle \(OCD\), we see that \(\quad OD = \cos(\alpha+\beta)\).
From triangle \(OFC\), we know \(\quad CF = \sin \beta \quad\) and \(\quad OF = \cos \beta.\)
From triangle \(CFG\), \[\sin \alpha = \frac{FG}{FC} \quad \Longrightarrow \quad FG = \sin \alpha \sin \beta.\]
From triangle \(OEF\), \[\cos \alpha = \frac{OE}{OF} \quad \Longrightarrow \quad OE = \cos \alpha \cos \beta.\]
As \(FG\) is equal in length to \(DE\), we have
\[\begin{align*} OE &= OD + DE \\ &= OD + FG. \\ \end{align*}\]Therefore \(\cos \alpha \cos \beta = \cos(\alpha+\beta) + \sin \alpha \sin \beta,\) so \(\cos(\alpha+\beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta,\) as required.
The restriction to acute angles is actually unnecessary - this works for all angles.
- By projecting the sides of an equilateral triangle onto a certain line, prove that \[\cos \theta + \cos \left(\theta + \frac{2\pi}{3}\right) + \cos\left(\theta+\frac{4\pi}{3}\right)=0\]
Let’s start by drawing an equilateral triangle inside a unit circle, at an angle \(\theta\) to the horizontal.
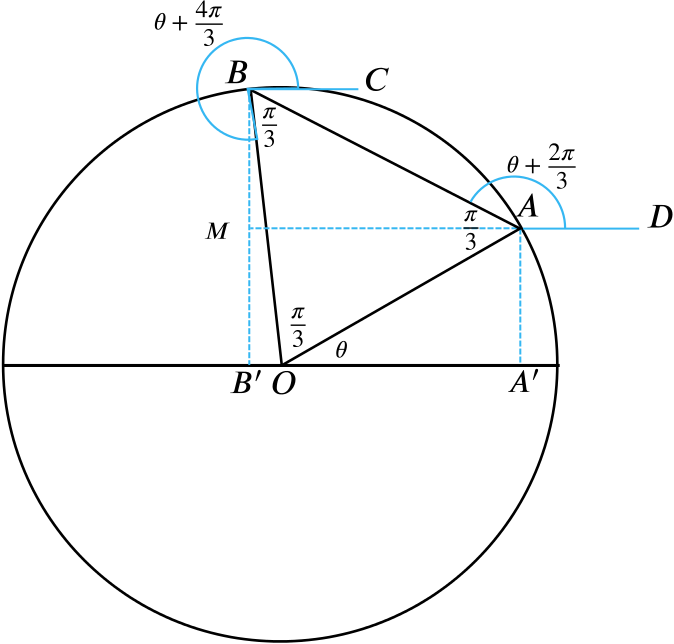
We can quickly identify (using parallel lines and angles in triangles) that \[\angle BAD = \theta + \frac{2 \pi}{3} \qquad \text{and} \qquad \angle CBO \text{ (reflex)} = \theta + \frac{4 \pi}{3}.\]
Thinking about the unit circle, we can see (by considering the diagrams below) that

If we take \(\psi = \theta + \dfrac{2 \pi}{3}\), we see that
\[\cos \left(\theta + \dfrac{2\pi}{3} \right) = \overrightarrow{AM} \equiv \overrightarrow{A'B'},\]
and taking \(\phi = \theta + \dfrac{4\pi}{3}\), we have
\[\cos \left(\theta + \dfrac{4\pi}{3} \right) = \overrightarrow{B'O}.\]
Therefore
\[\cos \theta + \cos \left(\theta + \frac{2\pi}{3} \right) + \cos \left(\theta + \frac{4\pi}{3} \right) = \overrightarrow{OA'} + \overrightarrow{A'B'} + \overrightarrow{B'O}.\]
(i.e. we move from \(O\) to \(A'\), return to \(B'\) and then back to \(O\)).
Therefore the total displacement is zero, and so \[\cos \theta + \cos \left(\theta + \frac{2\pi}{3}\right) + \cos\left(\theta+\frac{4\pi}{3}\right)=0.\]
…and find the value of the expression \[\sin \theta + \sin \left(\theta + \frac{2\pi}{3}\right) + \sin\left(\theta+\frac{4\pi}{3}\right).\]
The sum for \(\sin\) can similarly be found by projecting the sides of an equilateral triangle onto the \(y\)-axis.

We can think again about the unit circle and how we find the sine of different angles:

Let \(\psi = \theta + \dfrac{2\pi}{3}\) and \(\phi = \theta + \dfrac{4\pi}{3}\). From our diagram above, we get
\[\begin{align*} \sin \theta + \sin \left(\theta + \frac{2\pi}{3} \right) + &\sin \left(\theta + \frac{4\pi}{3} \right) \\ &= \overrightarrow{A'A} + \overrightarrow{MB} + \overrightarrow{BB'} \\ &= \overrightarrow{B'M} + \overrightarrow{MB} + \overrightarrow{BB'} \\ &= 0. \end{align*}\]
