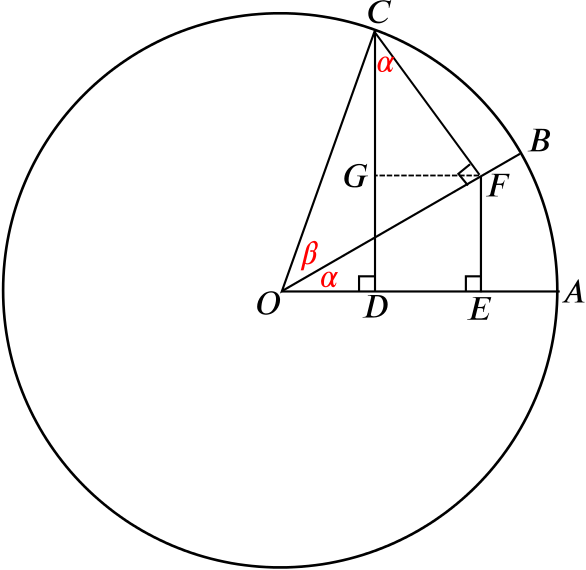
- Prove that \[\cos(A+B)=\cos A\cos B - \sin A\sin B,\] where the angles \(A\), \(B\) and \(A+B\) are all acute.
There is a standard geometric proof of this formula using the unit circle. If you haven’t come across it before, you may like to have a look at the diagram hidden below.
What lengths can you calculate, in terms of \(\alpha\) and \(\beta\)?
- By projecting the sides of an equilateral triangle onto a certain line, prove that \[\cos \theta + \cos \left(\theta + \frac{2\pi}{3}\right) + \cos\left(\theta+\frac{4\pi}{3}\right)=0\] and find the value of the expression \[\sin \theta + \sin \left(\theta + \frac{2\pi}{3}\right) + \sin\left(\theta+\frac{4\pi}{3}\right).\]
Could we draw an equilateral triangle at an angle \(\theta\) to the horizontal? What angles do we know? What horizontal lengths can we deduce?
To find the value of the \(\sin\) sum, what vertical lengths can we deduce?