Please note that we have used radians in this discussion, but we could have used degrees. The thinking and the ideas will be the same in both cases, so do try to read this even if you have used degrees.
Can you find …
- … two sine graphs which only cross each other on the \(x\)-axis?
Given that \(y=\sin x\) crosses the \(x\)-axis, what are the simplest transformations you could apply to it to obtain another sine graph which crosses the \(x\)-axis at the same points?
One option would be to reflect \(y=\sin x\) in the \(x\)-axis to give you the two sine graphs. Another would be to stretch it parallel to the \(y\)-axis.
- … a sine graph, a cosine graph and a tangent graph which all meet at certain points? What if all three graphs have to meet at the origin?
One approach could be to look at where two of \(y=\sin x\), \(y=\cos x\) and \(y=\tan x\) meet and then transform the third graph so that it also passes through these points.
For example, we could note that \(y=\sin x\) and \(y=\cos x\) meet at \(\big(\tfrac{\pi}{4}, \tfrac{\sqrt{2}}{2}\big)\), but \(\tan \tfrac{\pi}{4} = 1\), so we could rescale \(y=\tan x\) to give our third graph.
If we wanted to make sure all the graphs met at the origin, we could note that \(y=\sin x\) and \(y=\tan x\) meet at integer multiples of \(\pi\), so both pass through the origin. As \(y=\cos x\) passes through \((0,1)\) we could translate this graph to ensure that it also passes through the origin. We could think of using \(y= \cos ( x \pm \tfrac{\pi}{2})\), but what would the graphs look like in each case?
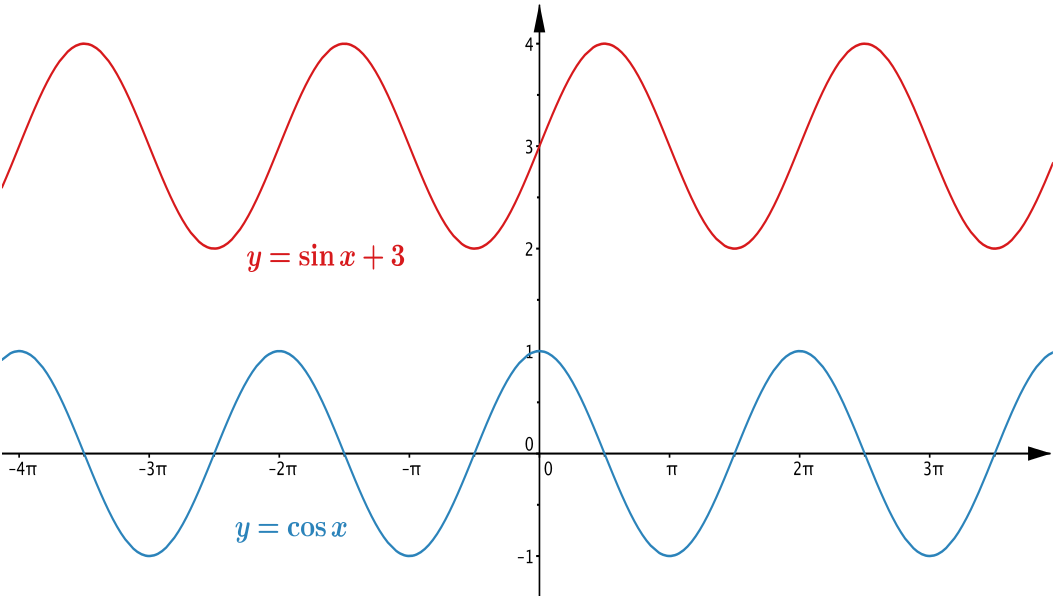
- … a sine graph and a cosine graph which don’t cross each other? What if the graphs have to lie between \(y=1\) and \(y=-1\)?
Here we should think about what “don’t cross each other” means. If we consider \(y=\cos x\) and \(y=\sin \left(x+ \tfrac{\pi}{2}\right)\), or \(y=\sin x\) and \(y=2-\sin x\) then the pairs of graphs don’t cross, but there are plenty of points in common. We will try to find graphs without any points in common. If we can’t manage to find graphs that will work, then we could allow the graphs to meet but not cross.
The graphs of \(y=\sin x\) and \(y=\cos x\) both take values between \(-1\) and \(1\). One option would be to slide one or both of the graphs parallel to the \(y\)-axis so that their values don’t overlap at all.
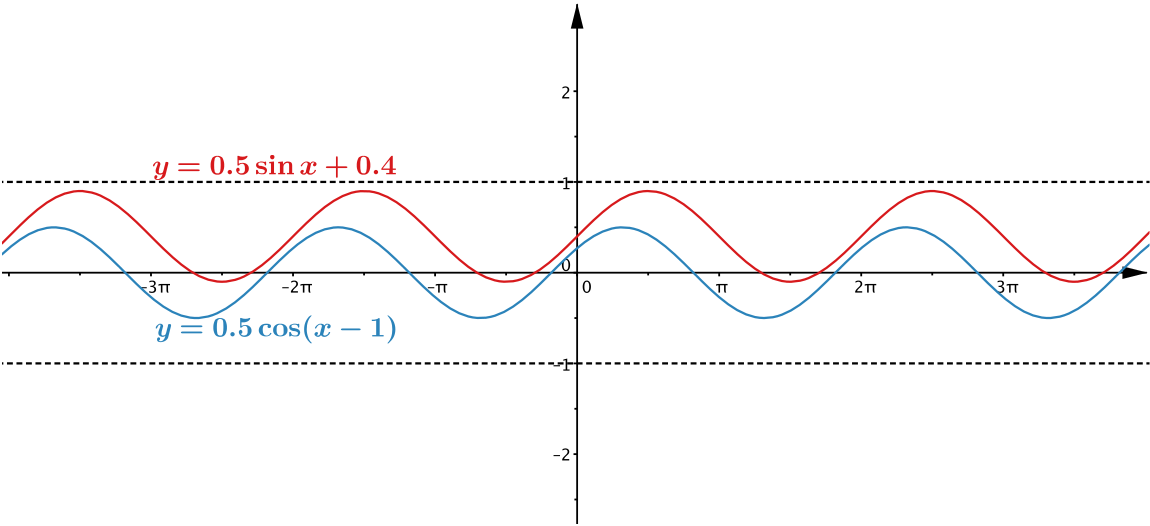
To solve the second part of the problem we could rescale the graphs so that they could be moved apart and still fit between the lines \(y=1\) and \(y=-1\). We could also combine this with translations parallel to the \(x\)- or \(y\)-axes so that the ranges of the functions overlap, but the graphs don’t actually cross. Here is one possible solution to illustrate this.
- … a cosine graph and a tangent graph which meet the \(x\)-axis the same number of times between \(x=-4\) and \(x=4\)? What if these points have to be the same for both graphs?
The graph of \(y=\tan x\) crosses the \(x\)-axis three times between \(x=-4\) and \(x=4\), whereas \(y=\cos x\) crosses the \(x\)-axis only twice in this interval. One option would be to translate the graph of \(y=\cos x\) so that it crosses the \(x\)-axis three times instead of two. Given that \(y=\sin x\) crosses the \(x\)-axis at the same points as \(y=\tan x\) and \(\sin x =\cos (x-\tfrac{\pi}{2})\), we could use \(y=\sin x\) and \(y=\tan x\) as our two graphs. A further option would be to increase the frequency of the cosine wave and then slide the graph down so that it just touches the \(x\)-axis.This could also give a cosine graph which meets the \(x\)-axis at the same points as the graph of \(y=\tan x\).

