How does an angular change on a Ferris wheel affect the height of a rider above the ground level?

We need to select a starting point - an initial position for the rider. It makes sense to choose this to be at the bottom of the wheel, where the rider first gets on. Once the wheel starts moving the rider will begin to move around the circumference of a circle. After some time the rider will have moved through an angle, \(\theta\), relative to the starting position and will be a height, \(h\), above the ‘ground’ (we are assuming that at the starting position the rider has a height of \(0\)).
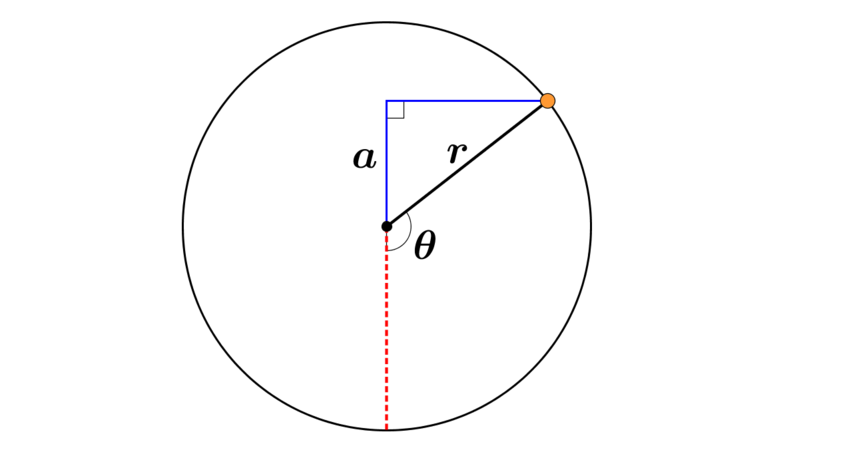
We can now add to our initial diagram, labelling the radius of the Ferris wheel, \(r\), and the angle through which the rider has turned, \(\theta\).
We are interested in finding the vertical height of the rider at this position. Notice that we can construct a right-angled triangle as shown in the following diagram.
Using trigonometry we can show that the length \(a\) is equal to \(r\cos \theta.\)
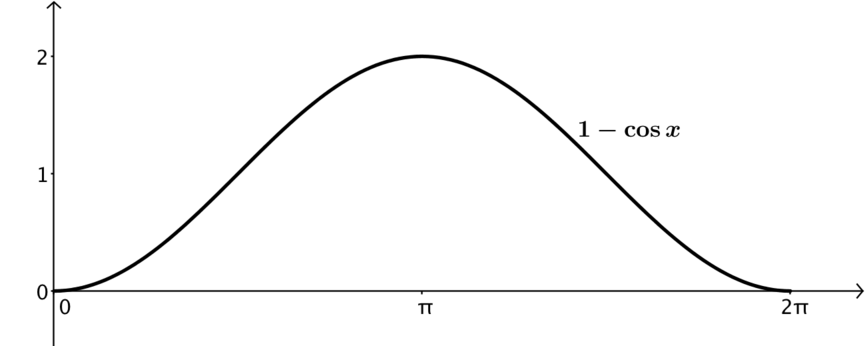
Then the vertical height of the rider above their starting position (the ground), \(h\), is \[r-r\cos \theta = r(1-\cos\theta).\]
It makes sense to check this result. We know that when \(\theta=0\), \(h\) should equal \(0\) and that when \(\theta=\pi\), \(h\) should equal \(2r\). Substituting \(\theta=0\) into our formula for the height gives \[h=r(1-\cos 0) = r(1 - 1) = 0,\] as required.
Similarly, substituting \(\theta=\pi\) into the formula for the height gives \[h=r(1-\cos \pi)=r(1-(-1)) = 2r.\]
We found this formula by considering the acute value of \(\theta\) in my original diagram. We have confirmed that the formula returns expected results for two specific values of \(\theta\) but it’s worth thinking a little further about why it works for all values of \(\theta\).
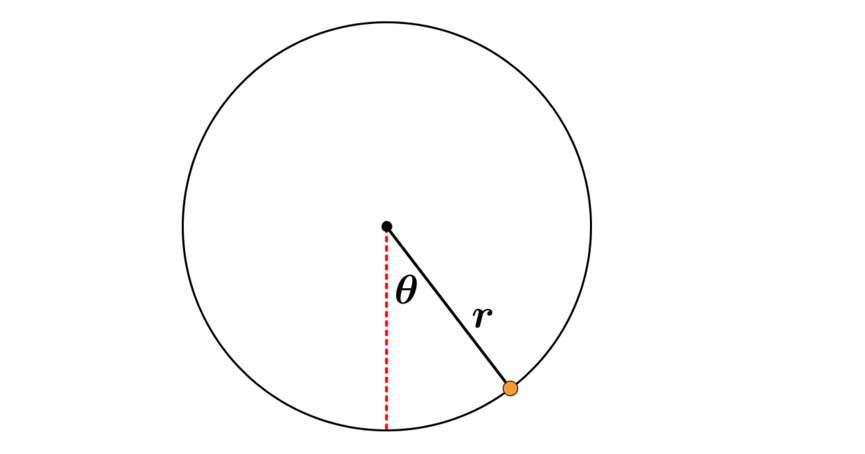
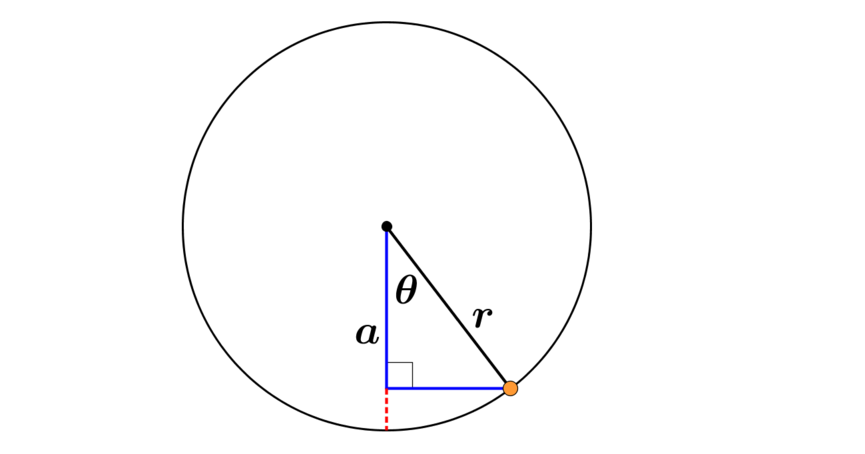
Consider the following two diagrams:
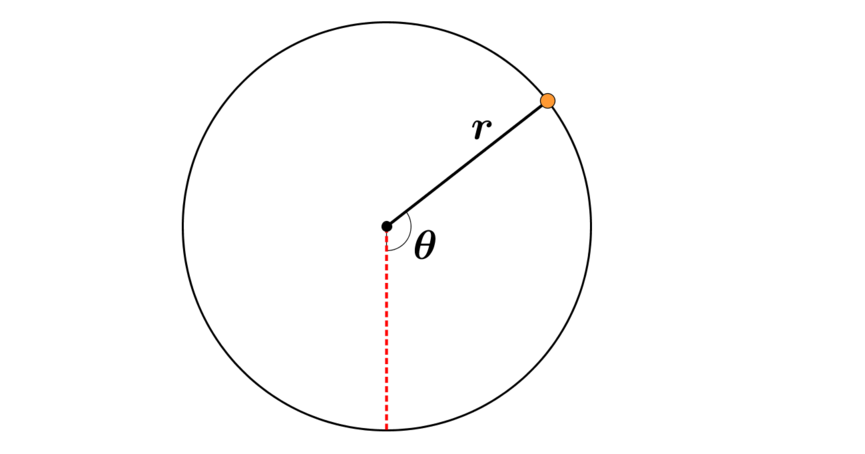
|
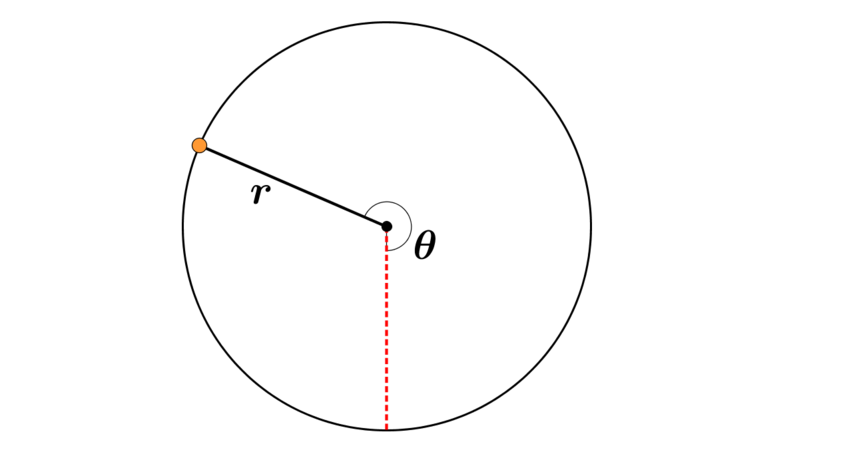
|
Can you use these diagrams to explain why the formula \(h=r(1-\cos\theta)\) also works for obtuse and reflex values of \(\theta\)?