The fraction of the interval \(0\leq x \leq 2\pi\), for which one (or both) of the inequalities \[\sin x \geq\frac{1}{2}, \qquad \sin 2x \geq \frac{1}{2}\] is true, equals
\(\frac{1}{3}\);
\(\frac{13}{24}\);
\(\frac{7}{12}\);
\(\frac{5}{8}\).
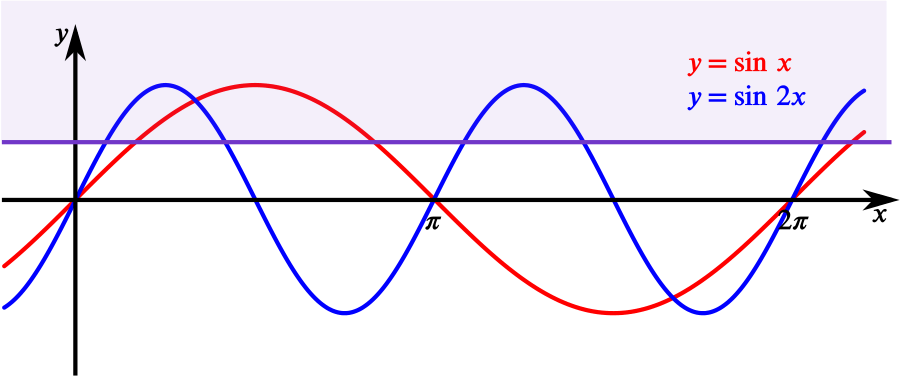
In the range \(0\leq x\leq2\pi\) we have \(\sin x\geq\dfrac{1}{2}\) if and only if \(\dfrac{\pi}{6}\leq x \leq \dfrac{5\pi}{6},\)
and \(\sin 2x\geq\dfrac{1}{2}\) if and only if \[\dfrac{\pi}{12}\leq x \leq \dfrac{5\pi}{12}\quad \text{or} \quad \dfrac{13\pi}{12} \leq x \leq \dfrac{17\pi}{12}.\]
So at least one of the inequalities holds for \(\dfrac{\pi}{12}\leq x \leq \dfrac{5\pi}{6}\) and \(\dfrac{13\pi}{12}\leq x \leq \dfrac{17\pi}{12}\).
The first of these intervals has length \(\dfrac{9\pi}{12}\) and the second has length \(\dfrac{4\pi}{12}\).
Therefore the fraction of the interval \(0\leq x \leq 2\pi\), for which one (or both) of the inequalities is true, is \(\dfrac{13\pi}{12}\) out of \(2\pi\), which is \(\dfrac{13}{24}\). Hence, the solution is (b).

