Exit fullscreen mode

Trigonometry: Triangles to Functions

Review question

How are these three angles connected?
Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Ref: R5497

Printable/supporting materials Printable version Fullscreen mode Teacher notes

Question

[Choose the one correct answer and explain your reasoning.]

The circle in the diagram has centre \(C\). Three angles \(\alpha, \beta, \gamma\) are also indicated.

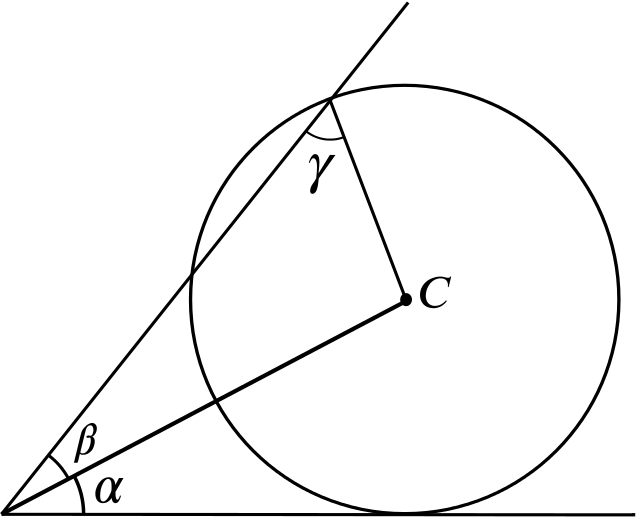
Circle with centre C. Alpha is the angle at a vertex A between a line segment tangent to the circle and a line segment ending at C. This line segment AC is also part of a triangle whose other vertex, B, lies on the circle and has angle gamma. The angle of the triangle at vertex A, adjacent to alpha, is beta.

The angles \(\alpha,\beta, \gamma\) are related by the equation:

\(\cos \alpha = \sin (\beta + \gamma)\),
\(\sin \beta = \sin \alpha \sin \gamma\),
\(\sin \beta (1 − \cos \alpha) = \sin \gamma\),
\(\sin (\alpha + \beta) = \cos \gamma \sin \alpha\).