The circle in the diagram has centre \(C\). Three angles \(\alpha, \beta, \gamma\) are also indicated.
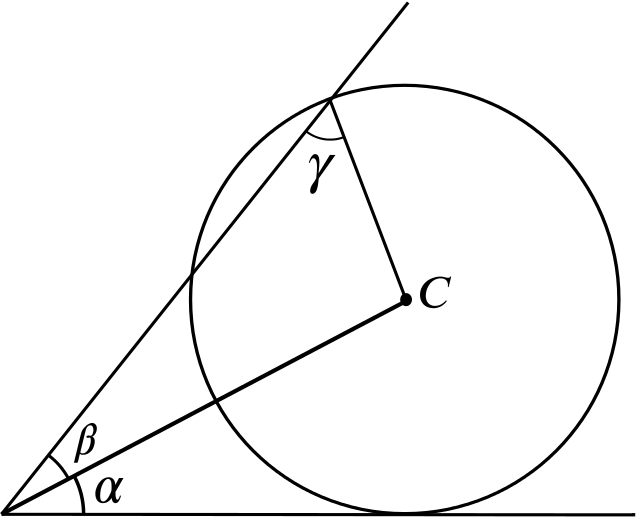
The angles \(\alpha,\beta, \gamma\) are related by the equation:
\(\cos \alpha = \sin (\beta + \gamma)\),
\(\sin \beta = \sin \alpha \sin \gamma\),
\(\sin \beta (1 − \cos \alpha) = \sin \gamma\),
\(\sin (\alpha + \beta) = \cos \gamma \sin \alpha\).
Let’s give the vertices in the diagram some names. We’ll call the vertex of angles \(\alpha\) and \(\beta\), \(A\), and the vertex of angle \(\gamma\), B.
We’ll also draw in the radius between C and the tangent - they’ll be perpendicular at the point of contact. We’ll call this point \(D\).
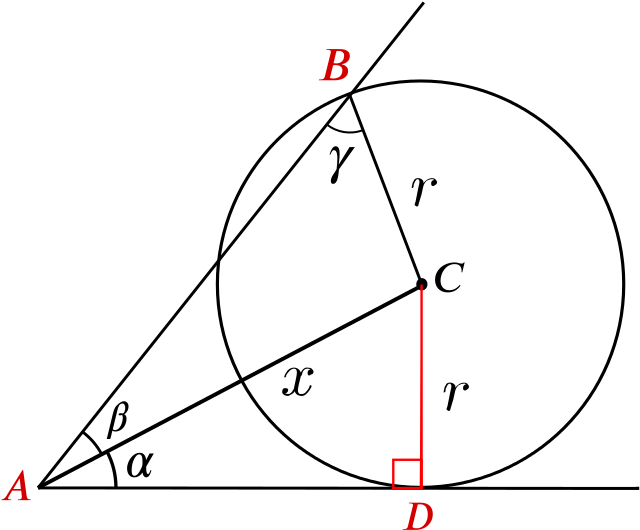
By looking at the right-angled triangle \(ACD\), we can see that the length of \(AC = x = \dfrac{r}{\sin \alpha}\), so \(r = x\sin\alpha\).
Now we can apply the sine rule to the triangle \(ABC\) to give \[\frac{\sin \beta}{r}=\frac{\sin \gamma}{x},\] so \[x\sin\beta = r\sin\gamma \implies x\sin\beta = x\sin\alpha\sin\gamma.\]
So on cancelling \(x\) we have \[\sin \beta = \sin \alpha \sin \gamma,\] and the answer is (b).

