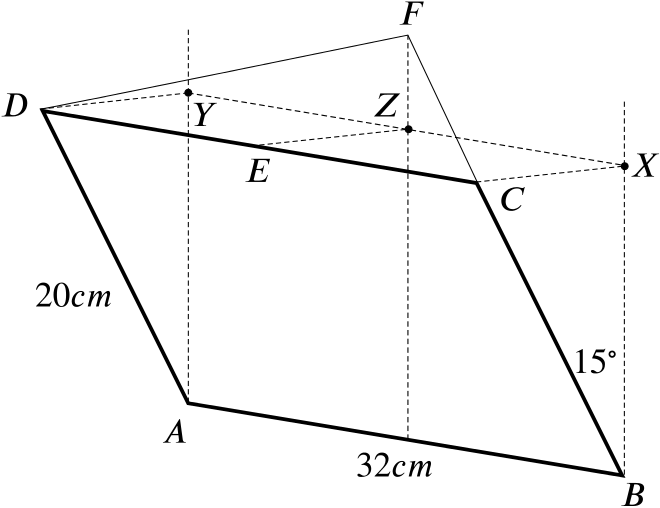
A rectangular picture of width \(\quantity{32}{cm}\) and height \(\quantity{20}{cm}\) has its lower edge \(AB\) horizontal against a vertical wall. It hangs at an angle of \(15^\circ\) to the wall and may be taken to be of negligible thickness. It is supported by two equal strings \(FD\), \(FC\) of length \(\quantity{20}{cm}\) attached to the upper corners \(C\), \(D\) of the picture and to a point \(F\) on the wall vertically above the centre of \(AB\).
Copy the given sketch, including the projections of \(C\), \(D\) and \(E\), the mid-point of \(CD\), onto the wall at \(X\), \(Y\) and \(Z\) respectively.
Identify in terms of the letters the following angles and calculate them:
- the angle between the two strings…
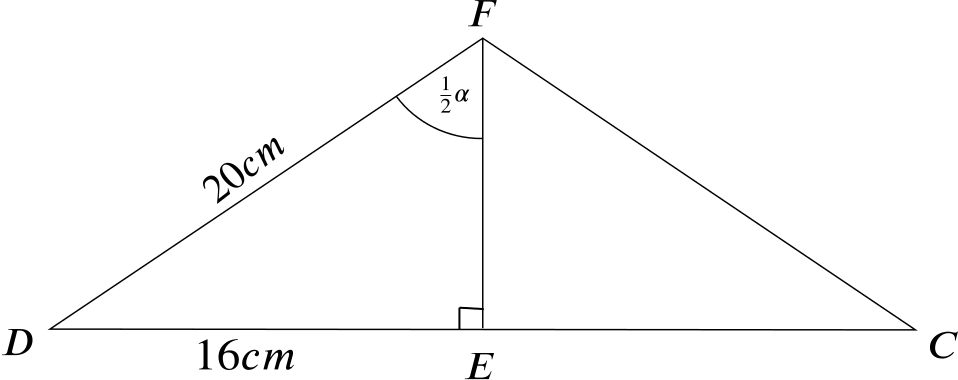
We know the length of two of the sides of the right triangle \(DEF\).
The angle between \(DF\) and \(FE\) is half the angle \(\alpha\) that we need, so we can use the definition of sine to give \[ \alpha = 2\sin^{-1} \frac{16}{20} \quad \left(=2\arcsin\frac{16}{20}\right) \quad \approx 106.3^\circ.\]
- the angle between the string \(DF\) and the wall…
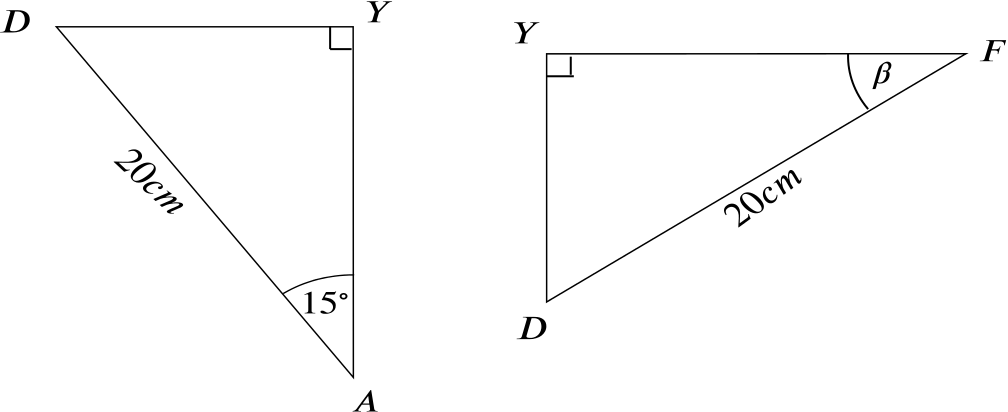
The angle between a line and a plane is given by the angle between the line and its perpendicular projection onto that plane, that is, the angle between the line \(DF\) and \(FY\).
So looking at the triangle \(AYD\), we can use the definition of cosine to find the length of \(YD\) as
\[20 \cos 15^\circ \approx \quantity{5.2}{cm}.\]
We can now obtain the angle \(\beta\) from the triangle \(FDY\) with help of the definition of the tangent, giving \[ \beta = \tan^{-1} (\cos 15^\circ) \quad (=\arctan(\cos15^\circ)) \quad \approx 14.5^\circ.\]
- the angle between the wall and the plane containing both strings.
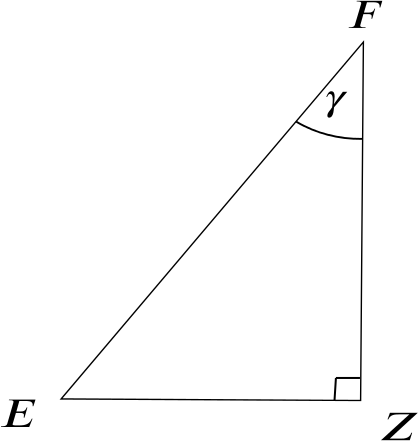
Let’s call the angle between the plane of the strings and the wall \(\gamma\), which is given by the angle between the lines \(FZ\) and \(FE\).
Looking at the triangle \(EFZ\), we can calculate the length of \(EF\) with help of Pythagoras as \(\sqrt{20^2-16^2} = 12\).
We also know that \(EZ\) has the same length as \(DY\), which we have already calculated. Finally we use the definition of sine again to obtain \[ \gamma = \sin^{-1} \frac{20 \cos 15^\circ}{12} \quad \left(=\arcsin\frac{20 \cos 15^\circ}{12}\right) \quad \approx 25.6^\circ.\]

