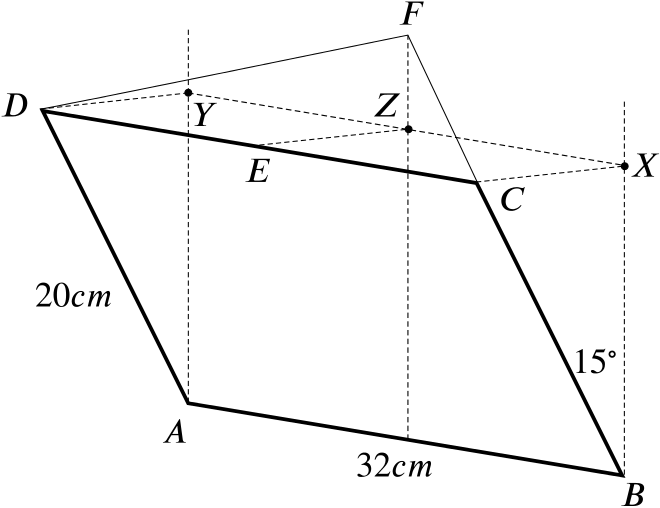
A rectangular picture of width \(\quantity{32}{cm}\) and height \(\quantity{20}{cm}\) has its lower edge \(AB\) horizontal against a vertical wall. It hangs at an angle of \(15^\circ\) to the wall and may be taken to be of negligible thickness. It is supported by two equal strings \(FD\), \(FC\) of length \(\quantity{20}{cm}\) attached to the upper corners \(C\), \(D\) of the picture and to a point \(F\) on the wall vertically above the centre of \(AB\).
Copy the given sketch, including the projections of \(C\), \(D\) and \(E\), the mid-point of \(CD\), onto the wall at \(X\), \(Y\) and \(Z\) respectively.
Identify in terms of the letters the following angles and calculate them:
- the angle between the two strings,
- the angle between the string \(DF\) and the wall,
- the angle between the wall and the plane containing both strings.
Are we certain about our definitions of trigonometric functions? And Pythagoras’ Theorem?
Can we look for useful triangles in the diagram where we can apply these rules?

