Two ships \(P\) and \(Q\) are simultaneously observed from two points \(X\) and \(Y\) on a straight coastline running from west to east. \(P\) is due north of \(X\) and lies on a bearing of \(300^\circ\) from \(Y\). \(Q\) is on a bearing of \(040^\circ\) from \(X\) and on a bearing of \(010^\circ\) from \(Y\). If the distance between \(X\) and \(Y\) is \(4\) miles, calculate the distance of the two ships from the shore.
Let’s start by drawing a picture.
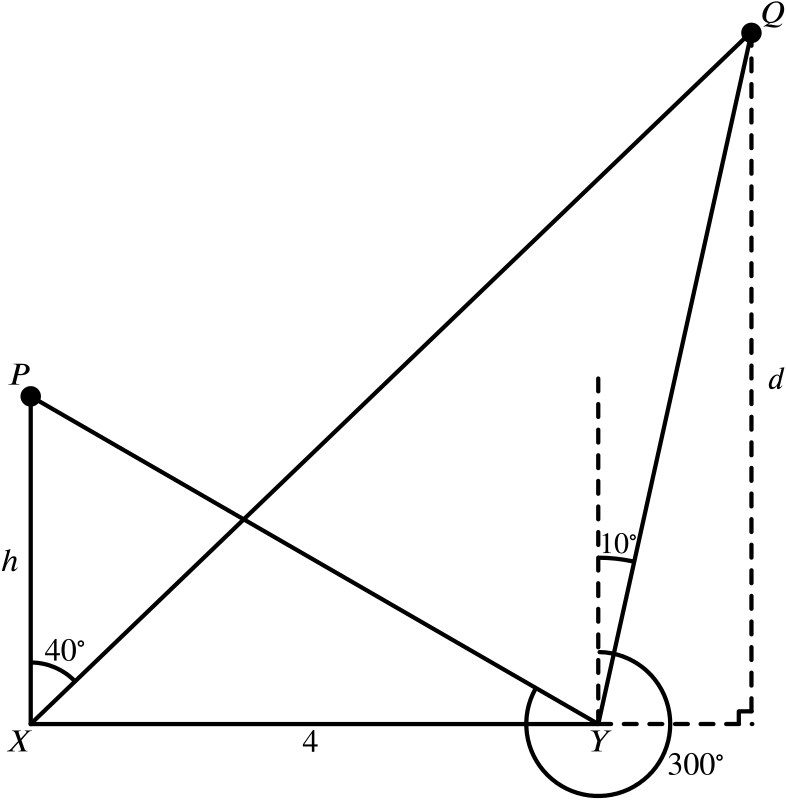
To find the distance of the ship \(P\) from the shore (labelled \(h\) in the diagram), let’s examine the right-angled triangle \(XPY\).
We can see that angle \(XYP=30^\circ\), and so \[h=4\times \tan 30=\frac{4}{\sqrt{3}}.\]
The distance of \(P\) from the shore is therefore \(\approx \quantity{2.31}{miles}\) (to \(3\)sf).
To find the distance of \(Q\) from the shore, \(d\), we need to work a bit harder. We can see from the diagram that \[d=XQ\times \sin 50,\] so if we can find the length \(XQ\) we are done.
Consider the triangle \(XYQ\). We know all the angles in this triangle and one of the side lengths, so let’s try the sine rule. This gives us that \[\frac{XQ}{\sin 100}=\frac{4}{\sin 30},\] and so \[XQ=\frac{4\sin 100}{\sin 30}=8 \sin 100.\]
Therefore \[d=XQ\sin 50=8\sin100 \sin50.\]
The distance of \(Q\) from the shore is therefore \(\approx \quantity{6.04}{miles}\) (to \(3\)sf).

