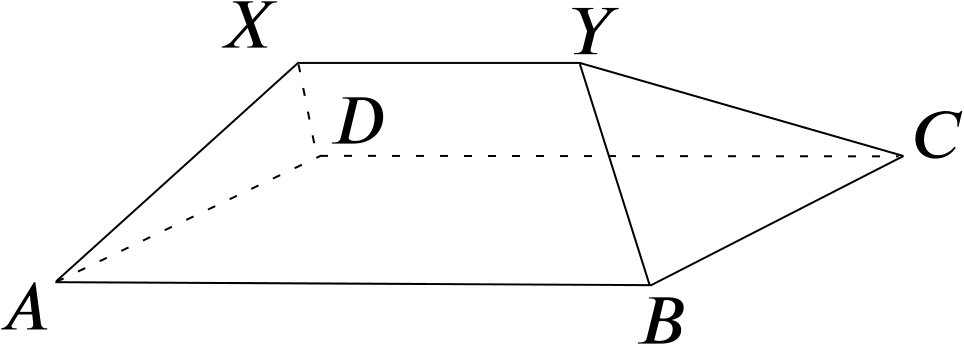
In the diagram, which represents the roof of a house, \(ABCD\) is a horizontal rectangle and \(XY\) a line parallel to \(AB\) and \(DC\). \(AB=40'\), \(BC=XY=16'\) and \(AX=BY=CY=DX=17'\). Calculate \((i)\) the height of \(XY\) above the plane \(ABCD\), …
Could we start by drawing a line perpendicular to \(ABCD\) through either \(X\) (or \(Y\))?
How could we calculate its length? Maybe we could construct a triangle containing this side?
… \((ii)\) the angle of inclination to the horizontal of the face \(AXYB\), and \((iii)\) the angle of inclination to the horizontal of the edge \(AX\).
Can we find more right-angled triangles which include one of these angles?

