We’ll drop the units in all calculations and keep in mind that all lengths are in feet.
In the diagram, which represents the roof of a house, \(ABCD\) is a horizontal rectangle and \(XY\) a line parallel to \(AB\) and \(DC\). \(AB=40'\), \(BC=XY=16'\) and \(AX=BY=CY=DX=17'\). Calculate \((i)\) the height of \(XY\) above the plane \(ABCD\), …
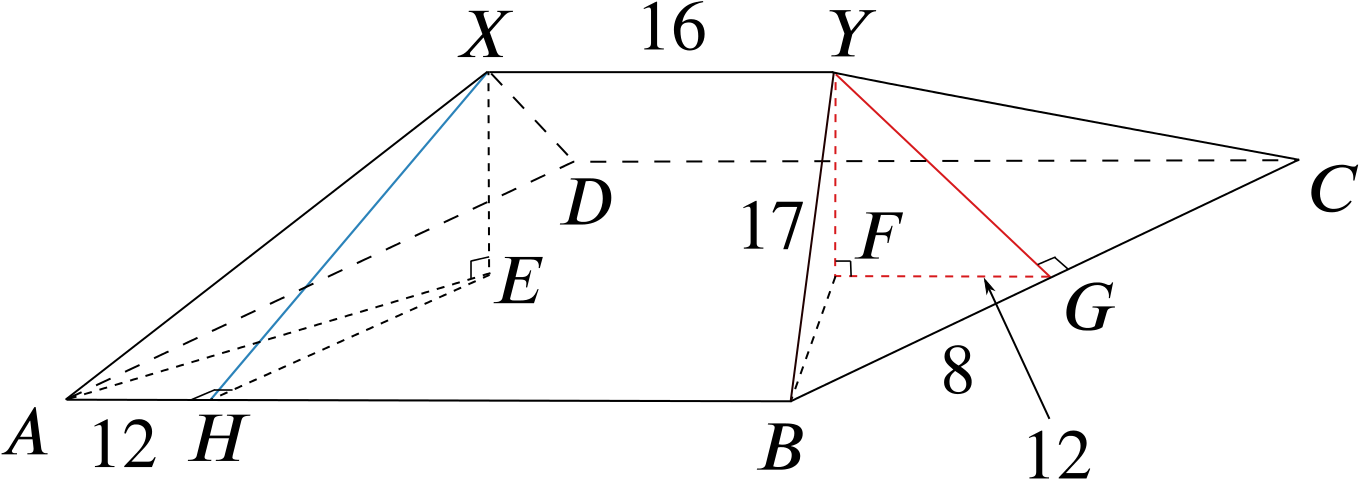
The height we want is \(FY\).
By using Pythagoras’ theorem on \(BGY\), we have \[GY= \sqrt{17^2-8^2}=15.\]\(8, 15\) and \(17\) is a Pythagorean triple. These often come up in questions about triangles and it can be really helpful to notice them.
Another example is \(3, 4\) and \(5\). Do you know any more?
In right-angled triangle \(GFY\) we have \(GF=12\) and the hypotenuse \(GY=15\) so \(GFY\) is similar to a triangle with sides \(3,4,5\) and thus \(FY=9.\)
If we don’t spot this we could use Pythagoras for a second time.
… \((ii)\) the angle of inclination to the horizontal of the face \(AXYB\), …
The desired angle is \(\angle XHE\). Looking at other lengths in the diagram, we can see that \(\tan(\angle XHE) = \dfrac{9}{8}\), and so \(\angle XHE = 48.3^\circ\).
… and \((iii)\) the angle of inclination to the horizontal of the edge \(AX\).
The desired angle is \(\angle XAE\). We can see that \(\sin(\angle XAE) = \dfrac{9}{17}\), and so \(\angle XAE = 32.0^\circ\).

