An equilateral triangle \(ABC\) has side length \(6\) units. The three altitudes of the triangle meet at \(N\). Show that \(AN=2\sqrt{3}\) units.
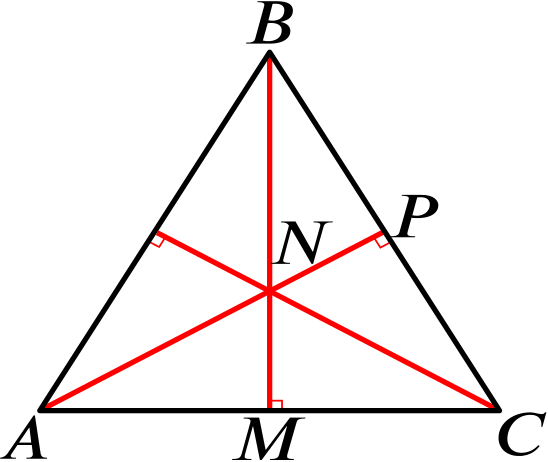
To find the length \(AN\), let’s call the midpoint of \(AC, M\), and the midpoint of \(BC, P\).
Then the triangles \(ANM\) and \(ACP\) are similar, since they are both right-angled, and they also share another angle.
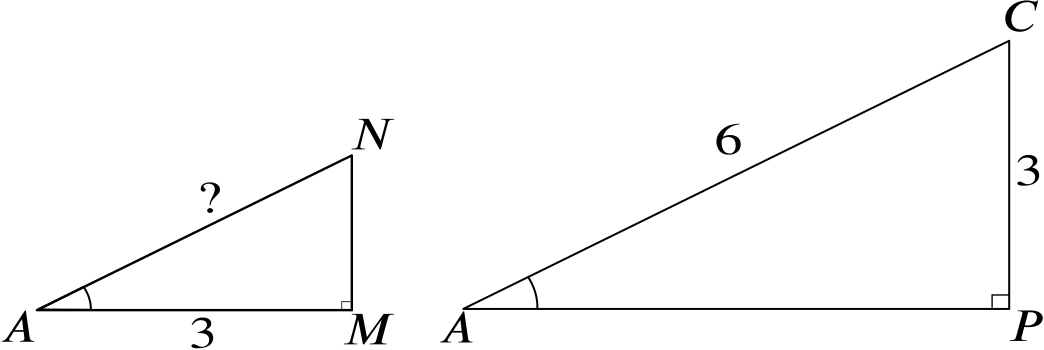
Using Pythagoras, we find that \(AP=\sqrt{6^2-3^2}=\sqrt{36-9}=\sqrt{27}=3\sqrt{3}\). We know that
\[\frac{AN}{3}=\frac{AN}{AM}=\frac{AC}{AP}=\frac{6}{3\sqrt{3}},\]
since the triangles are similar, and so \(AN=\dfrac{6}{\sqrt{3}}=6\dfrac{\sqrt{3}}{3}=2\sqrt{3}\) units.
Alternatively, we could have recognised that \(ANM\) is a standard \(30\)-\(60\)-\(90\) triangle with edges in the ratio \(1:2:\sqrt{3}\).
This triangle is the base of a pyramid whose apex \(V\) lies on the line through \(N\) perpendicular to the plane \(ABC\). Given that \(VN=2\) units, prove that \(\widehat{VAN}=30^\circ.\)
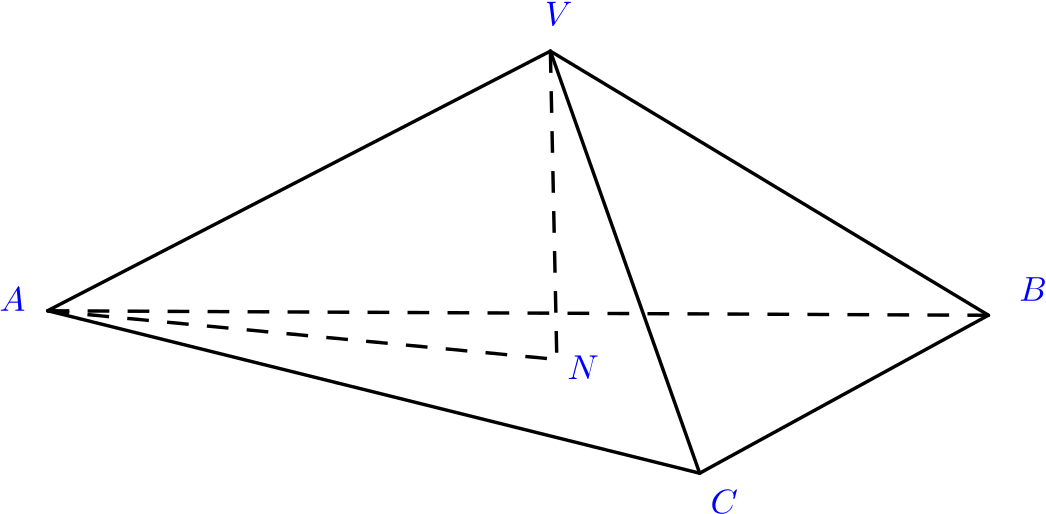
We know \(AN\), and \(VN\) is given in the question giving \(\tan\widehat{VAN}=\dfrac{2}{2\sqrt 3}=\dfrac{1}{\sqrt 3}\) which we should recognize as \(\tan 30^\circ\) giving \(\widehat{VAN}=30^\circ.\)
Alternatively we find \(AV = 4\), by Pythagoras.
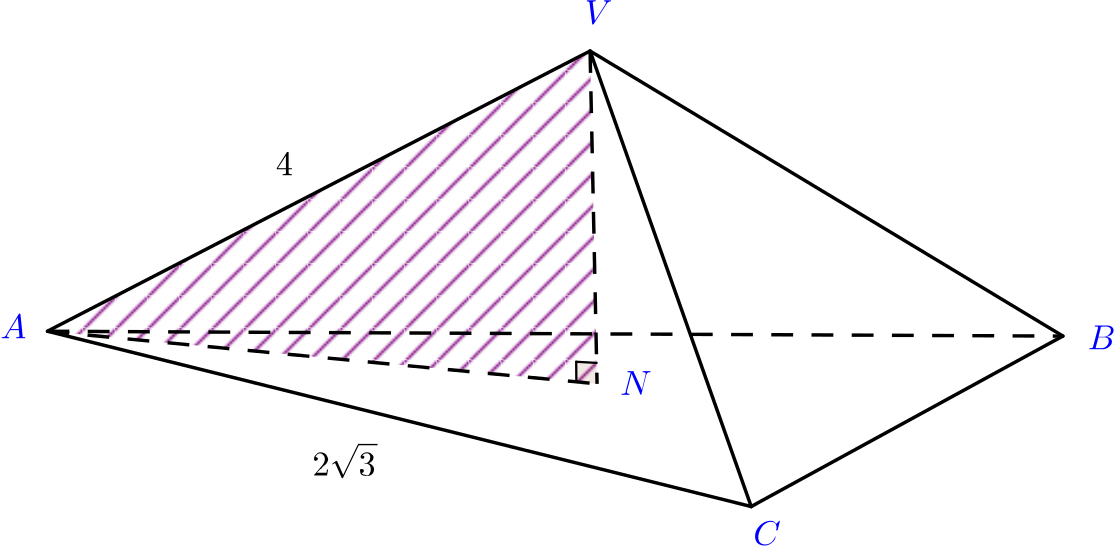
We now have that \[\sin\widehat{VAN}=\frac{2}{4}=\frac{1}{2},\] Therefore \(\widehat{VAN}=30^\circ.\)
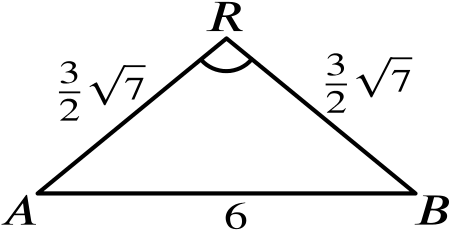
The perpendicular from \(A\) to the edge \(VC\) meets \(CV\) produced at \(R\). Prove that \(AR=\dfrac{3}{2}\sqrt{7}\) units, and find the exact value of \(\cos \widehat{ARB}\).
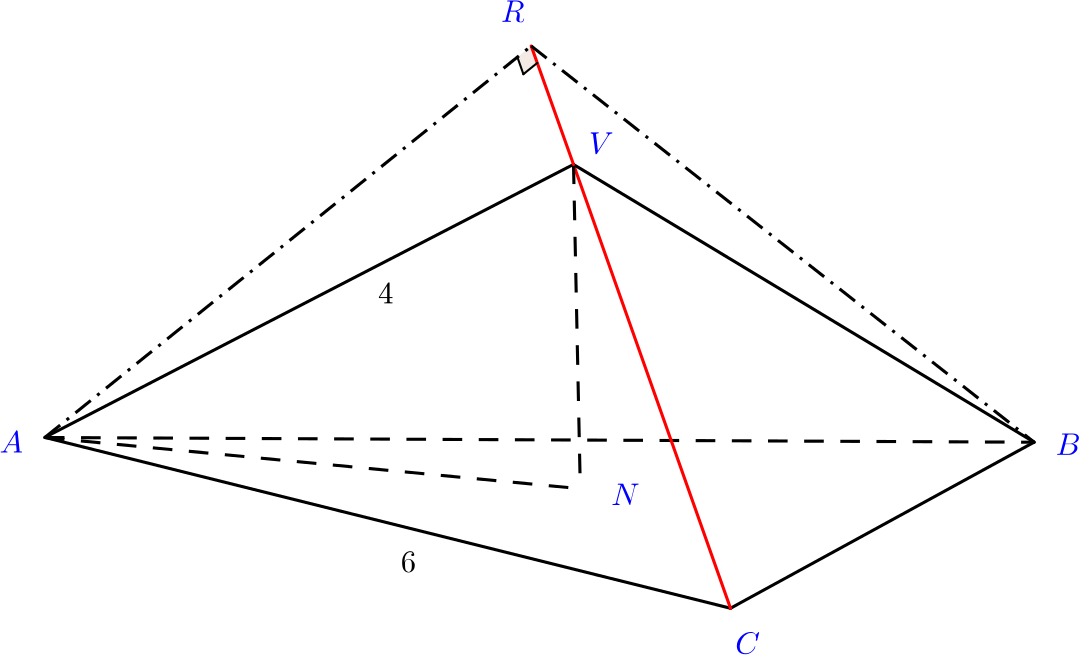
By symmetry, we know that \(AV=VC\). We’ll use the cosine rule to find \(\widehat{ACV}\).
Applying the cosine rule to \(ACV\), we have that \[\begin{align*} 4^2&=6^2+4^2-2\times 4\times 6\times \cos\widehat{ACV}, \\ 48\cos\widehat{ACV}&=36, \\ \cos\widehat{ACV}&=\frac{3}{4}. \end{align*}\]Now by right-angled trigonometry, we have that \[\sin\widehat{ACV}=\frac{AR}{6},\] and so \[AR=6\sin\widehat{ACV}=6\sqrt{1-\cos^2\widehat{ACV}}=6\sqrt{\frac{7}{16}}=\frac{6}{4}\sqrt{7}=\frac{3}{2}\sqrt{7}.\]
Alternatively, we could say \(RV = x\), and \(AR = y\), and then use Pythagoras twice to create simultaneous equations that enable us to find \(y\).
We need now to compute \(\cos\widehat{ARB}\).

By symmetry, we have that \(BR=AR\). So we can apply the cosine rule to \(ARB\).