- Given that \(\sin 3z^\circ = k\), where \(0 < k < 1\), how many values of \(z\) lie between \(0\) and \(360\)?
The function \(y=\sin 3z\) is a stretch of \(y=\sin z\:\), scale factor \(\dfrac{1}{3}\), in the \(x\)-direction.
Thus, instead of one ‘complete wave’ between \(0\) and \(360\), we have three, giving this graph:
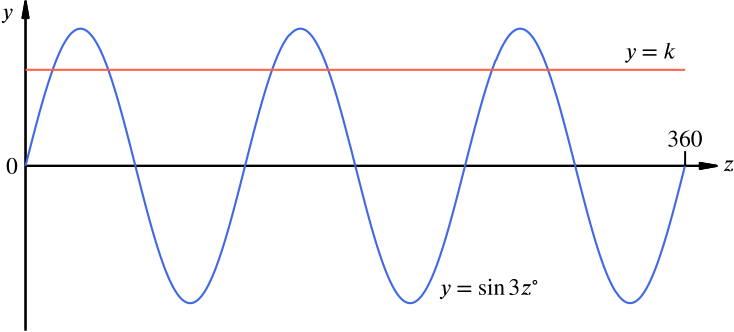
So while we would have two intersections between \(y = k\) and \(y = \sin z\) for \(0 < z < 360\), we’ll instead have six in the same interval.
- Given that \(X\) and \(Y\) both lie between \(0\) and \(360\), and that \(\sin X^\circ\) and \(\cos Y^\circ\) are both negative, find the values between which \(X + Y\) must lie.
If \(\sin X< 0\) and \(0 < X < 360\), then \(180 < X < 360\), while if \(\cos Y< 0\) and \(0 < Y < 360\), then \(90 < Y < 270\).
So for \(\sin X\) and \(\cos Y\) to both be negative, \(270 < X+Y < 630\).
Note that if \(270 < X+Y < 630\), this is no guarantee that \(\sin X\) and \(\cos Y\) are both negative (for example, \(X = 170, Y = 110\)).

