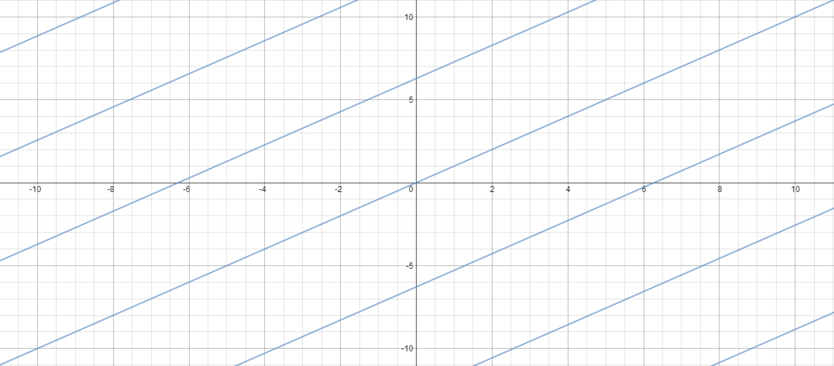
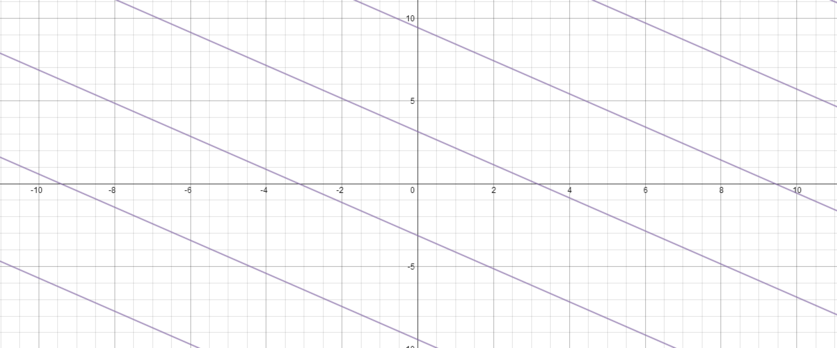
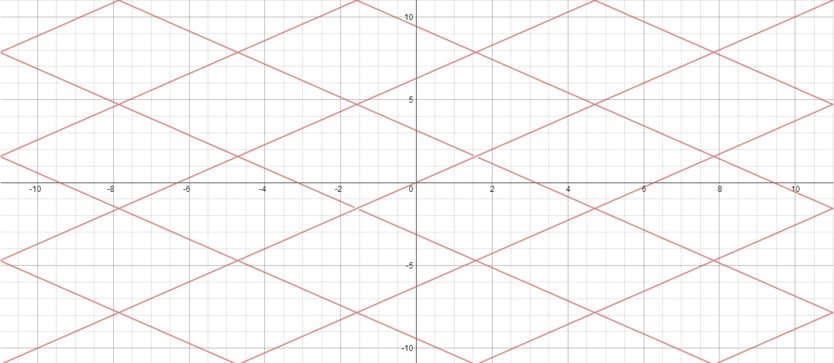
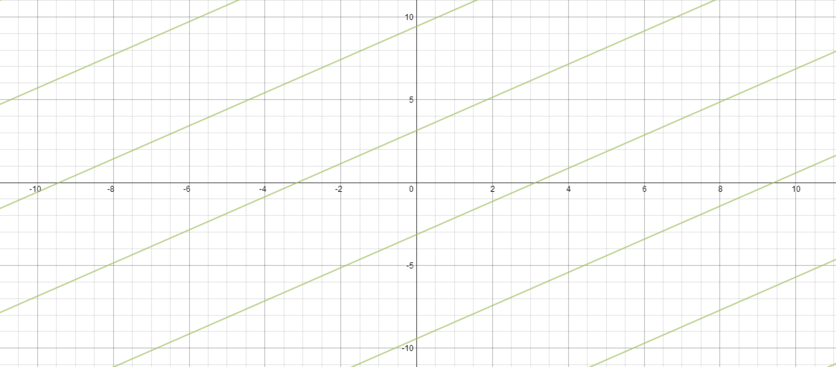
The graph of all those points \((x, y)\) in the \(xy\)-plane which satisfy the equation \(\sin(y) = \sin(x)\) is drawn in
|
|
|
|
|
|
Firstly, we know that the equation is trivially true when \(x=y\), and so we can rule out graphs (b) and (d) as the line \(y=x\) is missing.
Secondly, we know \(y = \pi - x\) is a solution to the equation, and this line does not appear in (d), which means that by elimination, (c) is the answer.
A fuller answer might run as follows: we know that for all values of \(x\), \[\sin(x)=\sin(\pi-x)\] and \[\sin(x)=\sin(x + 2n\pi),\] where \(n\) is an integer.
Thus if \(\sin(y) = \sin(x)\) then \[y = x + 2n\pi,\] OR \[y = \pi - x + 2n\pi = -x +(2n-1)\pi.\]
So the solution is given by the lines \[\cdots, y=x-2\pi, y = x, y = x+2\pi, y = x + 4\pi, \cdots,\] together with the lines \[\cdots, y = -x-\pi, y=-x+\pi, y=-x+3\pi, \cdots.\]
These are the lines shown in (c).