The angular elevation of the summit of a mountain is measured from three points on a straight level road. From a point due south of the summit the elevation is \(\alpha\), from a point due east of it the elevation is \(\beta\), and from the point of the road nearest to the summit the elevation is \(\gamma\).
If the direction of the road makes angle \(\theta\) east of north, prove that
- \(\tan\theta=\tan\alpha\cot\beta\)

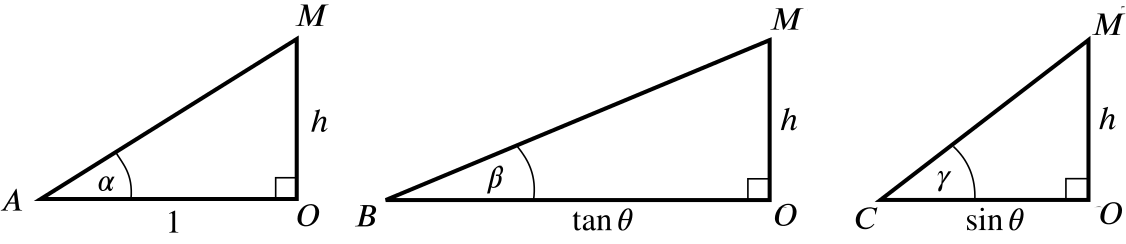
Let us choose the length \(AO\) to be \(1\), without loss of generality. (This says effectively that our angles will be the same whatever \(AO\) is.)
Let the height of the mountain be \(h\). We have three expressions for the height \(h\): \[\begin{align*} \triangle AOM:\quad h&=\tan\alpha\\ \triangle BOM:\quad h&=\tan\theta\tan\beta\\ \triangle COM:\quad h&=\sin\theta\tan\gamma. \end{align*}\]Equating \(h\) from triangles \(AOM\) and \(BOM\), we get \[h=\tan\alpha=\tan\theta\tan\beta\] so \[\tan\theta=\tan\alpha\cot\beta\] as required.
- \(\tan^2\gamma=\tan^2\alpha+\tan^2\beta\).
We will use here the identity \[1+\cot^2\theta=\cosec^2\theta.\]
We have from the diagrams
- \(\tan^2 \gamma = \dfrac{h^2}{OC^2}\)
- \(\tan^2\alpha = h^2\)
- \(\tan^2\beta = \dfrac{h^2}{OB^2},\) so
Find \(\gamma\), if \(\theta=31^{\circ}\) and \(\alpha=8^{\circ}\).
We can eliminate \(\beta\) from the results of (i) and (ii) to get \[\tan^2\gamma=\frac{\tan^2\alpha}{\sin^2\theta}.\] Substituting in the values for \(\theta\) and \(\alpha\), we find \(\gamma\approx15.3^\circ\).

