The vertices of an equilateral triangle are labelled \(X\), \(Y\) and \(Z\). The points \(X\), \(Y\) and \(Z\) lie on a circle of circumference \(10\) units. Let \(P\) and \(A\) be the numerical values of the triangle’s perimeter and area, respectively. Which of the following is true?
\(\dfrac{A}{P}=\dfrac{5}{4\pi}\);
\(P<A\);
\(\dfrac{P}{A}=\dfrac{10}{3\pi}\);
\(P^2\) is rational.
Since the circumference \(C=2\pi r=10\), we have \(r=\dfrac{5}{\pi}\).
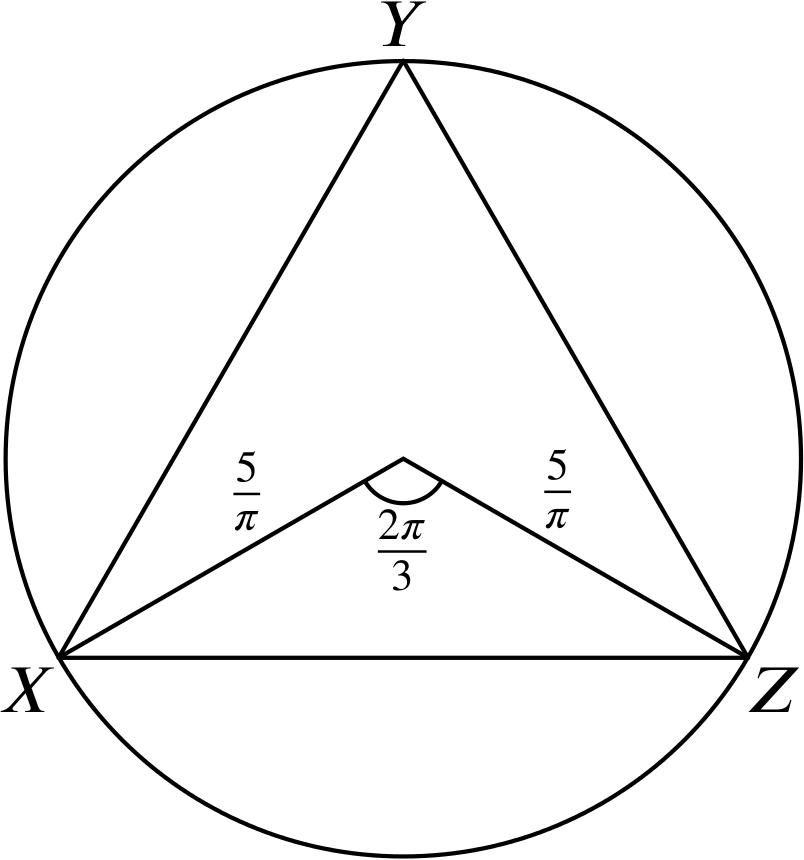
We know that the area of a triangle \(ABC\) is \(\dfrac{1}{2}ab\sin C\). Using this,the area of the smaller triangle shown in the diagram is \[\frac{1}{2}r^2\sin\left( \frac{2\pi}{3}\right)=\left(\dfrac{5}{\pi}\right)^2\frac{\sqrt3}{4} =\dfrac{25\sqrt{3}}{4\pi^2},\] since \(\sin\left( \dfrac{2\pi}{3}\right)=\dfrac{\sqrt{3}}{2}\).
Thus the area of the whole equilateral triangle is \[A=\dfrac{75\sqrt{3}}{4\pi^2}.\]
To find \(P\), we note that \[\dfrac{1}{2}XZ = r\sin \left(\frac{\pi}{3}\right)=\dfrac{5}{\pi}\frac{\sqrt{3}}{2},\] and hence \[P=\dfrac{15\sqrt{3}}{\pi}.\] Therefore \[\frac{A}{P}=\frac{75\sqrt{3}}{4\pi^2}\frac{\pi}{15\sqrt{3}}=\frac{5}{4\pi}\] so the answer is (a).
To check, it is easy to see that \(P^2\) is irrational, since it involves \(\pi^2\), so (d) is not correct.
Since \(\dfrac{A}{P} = \dfrac{5}{4\pi}, P > A\), so (b) is wrong.
From our work, (c) is clearly wrong.
Alternatively, the cosine rule applied to the smaller triangle could be used to find \(P\): \[P=3\times\sqrt{2\times r^2-2\times r^2\cos \left(\frac{2\pi}{3}\right)},\] which again gives \(P=\dfrac{15\sqrt3}{\pi}\).

