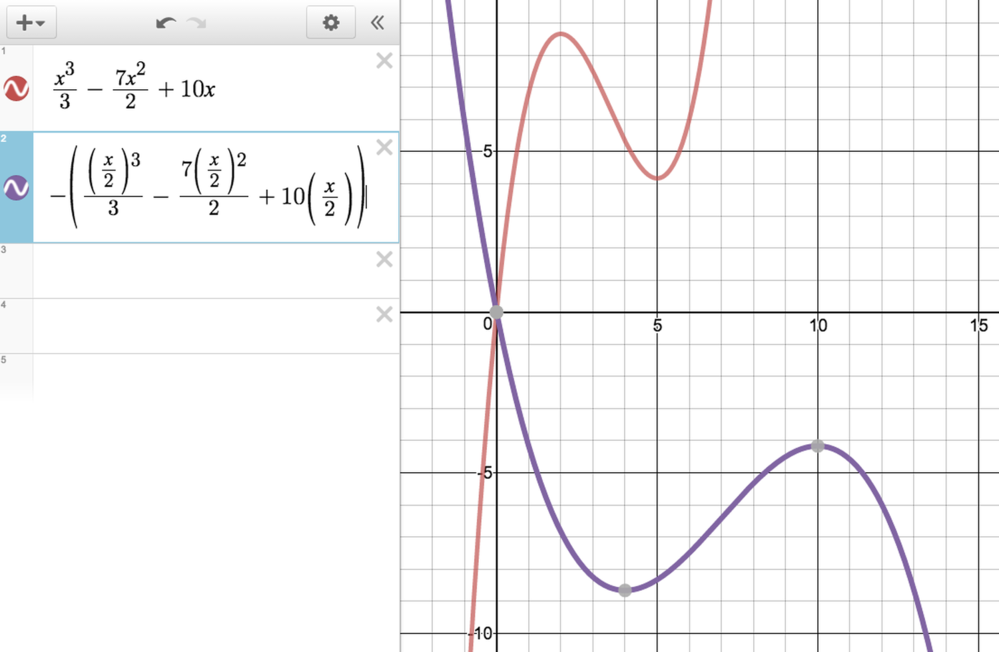
Here, we are going to use our knowledge of the calculus of cubic curves to help us to find some equations satisfying each of the conditions. That is, if \(f(x)\) is a cubic, what can we say about \(f'(x)\)?
Once we have an equation for our cubic curve we could use Desmos to check the features.
If you have an example that meets the conditions for one part of the problem
could you modify it to meet the conditions in a different part?
could you take a similar approach to a different part?
- … has no stationary points?
What does this mean for the derivative of the cubic function?
You might want to take a look at Curvy cubics.
- … has a stationary point when \(x=2\) and another when \(x=5\)?
If we want a cubic curve \(y=f(x)\) to have two stationary points, we know from calculus that \(f'(x)=0\) needs to have two distinct solutions. We can then use integration to give us possibilities for the cubic curve.
What could \(f'(x)\) look like if \(f'(x)=0\) has two distinct solutions?
- … has a local minimum when \(x=-1\)?
Can we create a cubic curve with a stationary point at \(x=-1\)? Could it be any type of stationary point? How many stationary points in total can we have for a cubic curve?
- … has a local minimum when \(x=-2\) and a local maximum when \(x=4\)?
What shape did the curve you created in part (b) have? Could we use this to help create a cubic curve with these conditions?
Student work
You may like to share one or two pieces of this sample student work during the task to help prompt discussion and encourage students to reflect on different ways to approach the problem.
Students A and B were working on part (c) of the problem. Student C was working on part (d) of the problem.
Student A
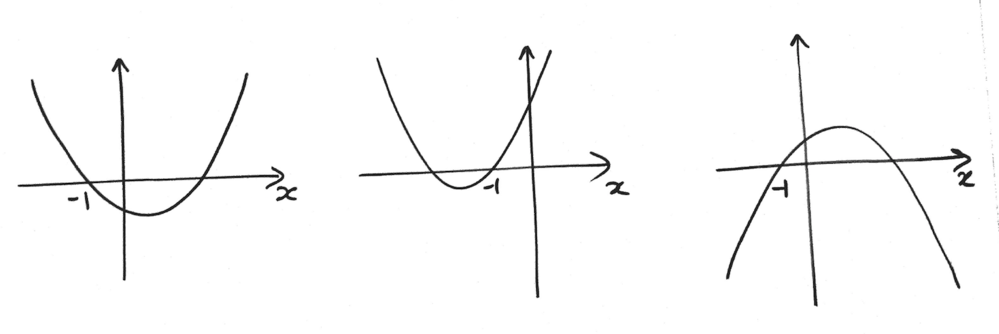
Student B
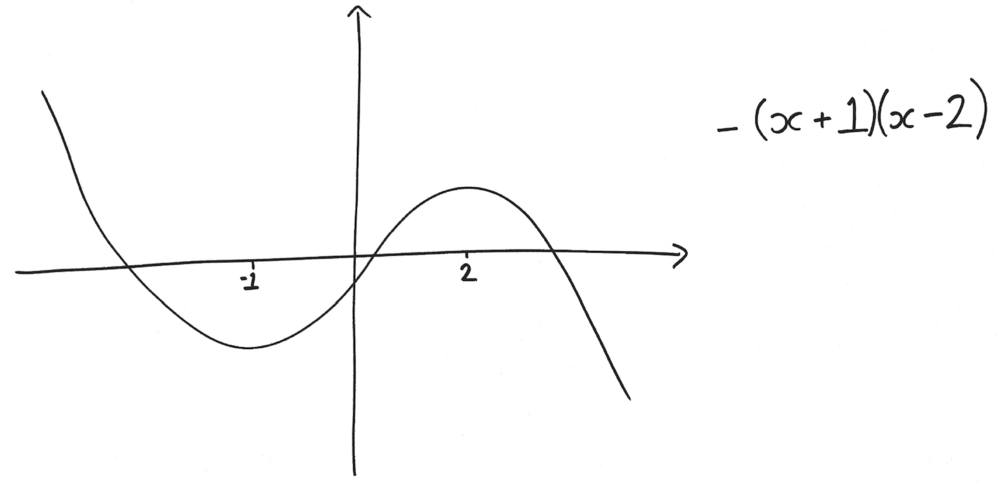
Student C