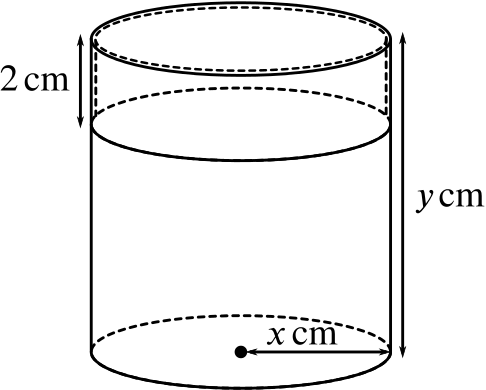
A cylindrical tin and its tight-fitting cylindrical lid (overlapping the tin by \(\quantity{2}{cm}\)) are to be made from thin sheet metal. When made, the total area of sheet metal used is \(\quantity{350\pi}{cm^2}\). The base radius of the tin is \(\quantity{x}{cm}\) and its height is \(\quantity{y}{cm}\) as shown in the diagram. Show that, neglecting the thickness of the metal, \[x^2+xy+2x=175.\]
Deduce that the volume, \(\quantity{V}{cm^3}\), of the tin is given by \[V= \pi(175x-2x^2-x^3).\]
If \(x\) may vary, find the values of \(x\) and \(y\) for which \(V\) has its maximum value.

